Groupes, logarithmes et confidentialité persistante

26 novembre 2020 — Cryptographie, Go, Diffie-Hellman

Le protocole TLS (anciennement SSL) permet de sécuriser les communications sur Internet — authentification, contrôle d’intégrité et confidentialité des échanges.

Ce protocole définit notamment un handshake au cours duquel client et serveur s’accordent sur le choix de la suite cryptographique à utiliser pour sécuriser la communication ultérieure et échangent des clefs cryptographiques.

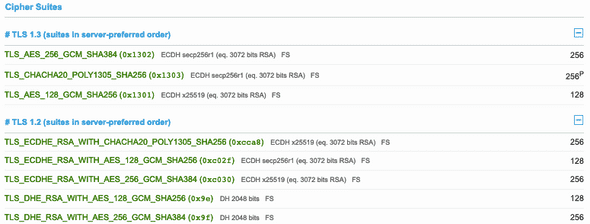
La page SSL Labs permet de scanner un serveur et de déterminer les versions de TLS et des suites cryptographiques (cipher suites) supportées.

Voici un extrait du résultat pour lipsum.dev :

On constate en particulier que le format des suites cryptographiques a changé avec TLS 1.3.

Dans la RFC 8446 qui définit ce protocole il est indiqué :

Static RSA and Diffie-Hellman cipher suites have been removed; all public-key based key exchange mechanisms now provide forward secrecy.

Nous proposons ici de présenter quelques notions mathématiques qui permettent la mise en oeuvre de cette confidentialité persistante (forward secrecy).

En particulier, TLS 1.3 repose sur des variantes d’un mécanisme d’échange de clefs imaginé en 1976 et utilisant des concepts mathématiques issus de la théorie des groupes.

Un peu de théorie

Une des caractéristiques des mathématiques est l’abstraction.

Cette abstraction consiste parfois à observer différents ensembles, les opérations associées et en déduire des structures communes.

L’une des structures algébriques les plus classiques est celle de groupe, qui intervient dans de nombreuses branches des mathématiques mais aussi en physique théorique, cristallographie, etc.

Structure de groupe

Un groupe est un ensemble $G$ muni d’une opération (notée ici $*$) qui permet d’effectuer des calculs sur cet ensemble en associant à deux éléments $a, b$ un troisième élément $c = a * b$ de $G$.

Pour que cette opération définisse une structure de groupe, on exige :

• l’opération est associative : $a * (b * c) = (a * b) * c$ (on omettra donc les parenthèses)
• il existe un élément neutre $e \in G$ tel que $g * e = e * g = g$ pour tout élément $g$ du groupe $G$
• les éléments de $G$ sont inversibles : pour tout $a \in G$, il existe $b \in G$ tel que ${a * b = b * a = e}$.
  Sous ces conditions, on montre que l’inverse est unique — je vous laisse le vérifier en exercice. On le notera $a^{-1}$, ou $-a$ lorsque l’opération du groupe est l’addition $+$.

Exemples

• L’ensemble $\Z$ muni de l’opération d’addition $+$ est un groupe.
  L’« inversion » de $n$ consiste alors à prendre son opposé $-n$.
• L’ensemble $\Bbb{Q}^{*}$ des nombres rationnels non nuls muni de l’opération de multiplication $\times$ est un groupe.
  L’inversion du nombre $\frac{a}{b}$ (avec $a, b$ entiers non nuls) donne alors $\frac{b}{a}$.

Exponentiation et logarithme

L’exponentiation en base $g$ consiste à appliquer l’opération $*$ de façon itérée à un élément $g$ d’un groupe $G$.

On définit ainsi $g^0 = e$ puis par récurrence $g^{n+1} = g * g^n$ pour $n \in \N$.

Exemples

• L’exponentiation de l’addition sur $\Z$ correspond à la multiplication, par exemple : ${a + a + a + a = 4a}$ ($a$ désignant un entier quelconque)
• La notation avec un exposant est réservée à l’exponentiation de la multiplication, qui correspond à la classique « puissance n-ème » : ${a \times a \times a \times a = a^4}$

Exponentiation rapide

Pour calculer $g^n$, on peut naïvement effectuer des multiplications successives pour calculer la suite $g, g^2, g^3, ..., g^n$.

Si l’on procède ainsi, le nombre de multiplications à effectuer est $n-1$.

Il existe une approche beaucoup plus efficace qui consiste à multiplier les résultats intermédiaires par eux-mêmes.

Par exemple, pour calculer $h = g^{42}$, on peut remarquer que ${42 = 101010_2}$ (notation binaire) puis :

• On part de $h = e$ (élément neutre)
• On calcule successivement $g, g^2, g^4 = {(g^2)}^2, g^8 = {(g^4)}^2, g^{16} = {(g^8)}^2, g^{32} = {(g^{16})}^2$, en multipliant $h$ par $g^{2^k}$ à l’étape $k$ si le bit correspondant en notation binaire est à $1$.
• Le nombre obtenu est dans notre cas $g^2 * g^8 * g^{32} = g^{42}$.

Ce calcul fait intervenir $5$ multiplications au lieu des $41$ de la méthode naïve. Pour un exposant $n$, ce nombre de multiplications est de l’ordre de $\log_2(n)$.

Notons que cet algorithme d’exponentiation rapide ne fait aucune hypothèse sur le groupe dont il est question ni sur la loi de composition $*$.

💻  En voici une implémentation (en Go), dans le cas classique de la multiplication des entiers :

// Computes a^n in O(log n) steps
func Exponentiate(a int, n int) int {
	res := 1
	for n > 0 {
		if n%2 == 1 {
			res *= a
			n = (n - 1) / 2
		} else {
			n /= 2
		}
		a *= a
	}
	return res
}

Logarithme

Pour un groupe $G$ et un élément $g$ de ce groupe, le problème du logarithme en base $g$ consiste à résoudre l’équation $g^n = h$ d’inconnue $n$.

Suivant les cas, il existera zéro, une ou plusieurs solutions $n$ à cette équation — parfois une infinité.

Groupes cycliques

Un groupe cyclique est un cas particulier de groupe qui a les propriétés additionnelles suivantes :

• $G$ est fini, on notera $n$ son nombre d’éléments.
• $G$ est monogène, c’est-à-dire qu’il existe un élément $g$ à partir duquel on peut obtenir tous les autres par exponentiation.

On a alors ${G = \{g^0, g^1, ..., g^{n-1}\}}$ et nécessairement (je vous laisse le prouver) $g^n = g^0 = e$.

Calcul du logarithme discret

Le logarithme (discret) en base $g$ sur un groupe cyclique $G$ à $n$ éléments et généré par $g$ peut être défini comme une fonction $\log_g: G \to \{0, 1, ..., n - 1 \}$ qui vérifie $g^{\log_g(h)} = h$ pour tout $h \in G$.

Cette relation ne donne a priori ni formule explicite de calcul ni algorithme autre qu’une méthode par force brute consistant à tester successivement avec $0, 1, 2, ..., n - 1$.

On effectue alors en moyenne de l’ordre de $n$ opérations d’exponentation.

Il est cependant possible de le calculer de façon plus efficace :

• sur n’importe quel groupe cyclique, par exemple avec l’algorithme baby-step giant-step que nous décrivons ci-dessous
• ce nombre d’opérations peut encore être réduit si la décomposition de $n$ en produit de nombres premiers vérifie certaines conditions (algorithme de Pohlig-Hellman)
• sur des cas particuliers de groupes, d’autres considérations peuvent amener à réduire drastiquement la complexité du problème

💡 Algorithme « Baby-step giant-step »

Ce paragraphe visant à présenter cet algorithme est facultatif, vous pourrez librement y revenir ensuite.

Cet algorithme proposé en 1971 permet d’obtenir $\log_g(h)$ en un nombre d’opérations de l’ordre de $\sqrt{n}$.

Notons $G = \{g^0, g^1, ..., g^{n-1}\}$ un groupe cyclique à $n$ éléments et $N$ l’arrondi supérieur de $\sqrt{n}$ (noté $N = \lceil \sqrt{n} \rceil$).

Définissons alors :

• $\textnormal{Babies} = \{ 0, 1, 2, ..., N-1 \}$ les entiers de $0$ à $N-1$ par pas de $1$
• $\textnormal{Giants} = \{ 0, N, 2N, ..., (N-1)N \}$ les entiers de $0$ à $(N-1)N$ par pas de $N$

L’application $f: \textnormal{Babies} \times \textnormal{Giants} \to G$ définie par $f(i, j) = g^{i + j}$ est surjective.

Je vous laisse vous en convaincre en exercice, en considérant pour $g^k \in G$ quelconque la division euclidienne de $k$ par $N$.

$f(i, j) = h$ équivaut à résoudre $g^i * g^j = h$ soit $g^i = h * g^{-j}$

On est donc amené à chercher une collision entre les séquences $(g^i)_{i \in \textnormal{Babies}}$ et $(h*g^{-j})_{j \in \textnormal{Giants}}$, qui contiennent chacun $N = \lceil \sqrt{n} \rceil$ éléments.

On sait résoudre ce problème en $O(\sqrt{n})$ opérations (par exemple avec une table de hachage).

Les indices $i, j$ obtenus vérifient alors $g^{i + j} = h$ ce qui résoud le problème du logarithme discret.

Échange de clés Diffie-Hellman

En 1976 est publié un article intitulé New Directions in Cryptography.

Cet article définit l’un des premiers mécanismes cryptographiques d’échange de clef, qui porte le nom d’échange de clés Diffie-Hellman.

Ce mécanisme permet à deux personnes, que nous appellerons Amandine et Bastien, d’établir une clef secrète S que eux seuls connaissent en échangeant sur un canal non sécurisé.

Nous verrons plus loin comment ce mécanisme est utilisé en pratique dans le protocole TLS.

Description de l’échange

1. Amandine et Bastien ont choisi un groupe cyclique $G$ de taille $n$ et un générateur $g$ de ce groupe — ces données sont publiques.
   Le groupe $G$ étant fini, on peut encoder ses éléments sous forme de nombres de taille définie.
2. Amandine génère un entier aléatoire $a$, avec $0 < a < n$. Elle conserve secrètement $a$ et transmet à Bastien $g^a$ (sur le canal non sécurisé).
3. De même, Bastien génère un entier aléatoire $b$, avec $0 < b < n$. Il conserve secrètement $b$ et transmet à Amandine $g^b$ (sur le canal non sécurisé).
4. Bastien utilise sa clef secrète $b$ pour calculer $(g^a)^b = g^{ab}$.
5. Amandine utilise sa clef secrète $a$ pour calculer $(g^b)^a = g^{ba} = g^{ab}$.

À l’issue de cet échange, Amandine et Bastien ont tous deux connaissances du secret partagé ${S = g^{ab}}$.

Robustesse

Les clefs $g^a$ et $g^b$ circulant sur des canaux non sécurisés, elles peuvent être utilisées par une tierce personne pour tenter d’obtenir le secret $S$.

Si cette personne est capable de calculer l’un des logarithmes discrets $\log_g(g^a)$ ou $\log_g(g^b)$, elle peut alors obtenir l’un des exposants secrets $a$ ou $b$ et recalculer $S$.

La résolution du logarithme discret est donc un vecteur d’attaque potentiel contre le mécanisme de Diffie-Hellman.

Bien que cela ne soit pas prouvé dans le cas général, on considère d’ailleurs que Diffie-Hellman est aussi sûr que le problème du logarithme discret.

La difficulté de calcul du logarithme sera donc déterminante dans le choix du groupe cyclique utilisé en pratique.

💻 Implémentation avec Golang

⚠️ Les implémentations naïves présentées dans cet article ne doivent évidemment pas être utilisées en production, leur but est purement didactique.

Nous proposons ci-dessous une implémentation avec différents groupes cycliques.

Cette implémentation est écrite en Go, dont nous utiliserons le module crypto, mais il n’est pas nécessaire d’être familier avec ce langage pour lire la suite.

Une interface CyclicGroup

L’interface ci-dessous définit ce qu’on attendra d’une implémentation d’un groupe cyclique.

On y retrouve les notions suivantes :

• Identity, Compose, Inverse qui correspondent aux axiomes d’un groupe (élément neutre, loi de composition interne et inversion)
• Order, Generator qui correspondent au cas d’un groupe cyclique

type CyclicGroup interface {
	Identity() interface{}
	Compose(a, b interface{}) interface{}
	Inverse(a interface{}) interface{}
	Exponentiate(a interface{}, exp *big.Int) interface{}
	Generator() interface{}
	Order() *big.Int
	String() string
}

💡 On a utilisé des empty interface (qui peuvent contenir n’importe quelle valeur) pour typer les éléments du groupe, dont nous ne savons rien a priori. Dans d’autres langages, on pourrait utiliser des types génériques (inexistant en Go).

Groupe multiplicatif modulo p

Rappelons quelques définitions vues dans un article précédent.

On note $\Z/n\Z$ l’ensemble des nombres entiers modulo $n$ ($n$ désigne un entier positif quelconque).

Compter dans $\Z/n\Z$ revient à compter avec les nombres $\{0, 1, ..., n - 1\}$ en considérant tous les calculs comme effectués modulo $n$.

Par exemple, modulo $7$, on a ${5 \times 5 = 25 = 4}$ et la table de multiplication de $\Z/7\Z$ est la suivante :

x	0	1	2	3	4	5	6
0	0	0	0	0	0	0	0
1	0	1	2	3	4	5	6
2	0	2	4	6	1	3	5
3	0	3	6	2	5	1	4
4	0	4	1	5	2	6	3
5	0	5	3	1	6	4	2
6	0	6	5	4	3	2	1

On sait que lorsque $p$ est un nombre premier les éléments de $\Z/p\Z$ différents de $0$ sont tous inversibles pour la multiplication : $\Z/p\Z$ est un corps que l’on notera aussi $F_p$.

On remarque également sur ce particulier que $3$ permet de générer les $6$ éléments non nuls de $\Z/7\Z$ :
$3^0 = 1$, $3^1 = 3$, $3^2 = 9 = 2$, $3^3 = 6$, $3^4 = 4$, $3^5 = 5$.

De fait, on montre qu’il existe toujours au moins un nombre dans $F_p$ qui permet de générer tous les éléments non nuls par exponentiation, comme c’est le cas de $3$ dans $F_7$.

Un tel nombre est appelé une racine primitive modulo $p$.

Dès lors, l’ensemble des éléments non nuls de $F_p$ muni de la multiplication est un groupe cyclique, d’ordre $p-1$.

Implémentation de MultGroup

Voici ci-dessous une implémentation très simple des groupes multiplicatifs modulo $p$.

Notons que l’on utilise le type big.Int pour manipuler des entiers de taille arbitraire.

type MultGroup struct {
	P   *big.Int
	Gen *big.Int
}

func (group *MultGroup) Order() *big.Int {
	// P - 1
	return new(big.Int).Add(group.P, big.NewInt(-1))
}

func (group *MultGroup) Identity() interface{} {
	return big.NewInt(1)
}

func (group *MultGroup) Compose(a, b interface{}) interface{} {
	// a * b % P
	return new(big.Int).Mod(
		new(big.Int).Mul(a.(*big.Int), b.(*big.Int)),
		group.P,
	)
}

func (group *MultGroup) Inverse(a interface{}) interface{} {
	return new(big.Int).ModInverse(a.(*big.Int), group.P)
}

func (group *MultGroup) Exponentiate(a interface{}, exp *big.Int) interface{} {
	return new(big.Int).Exp(a.(*big.Int), exp, group.P)
}

func (group *MultGroup) Generator() interface{} {
	return group.Gen
}

💡 On utilise l’exponentiation modulaire des entiers implémentée nativement en Go, plus efficace que l’exponentiation rapide générique présentée précédemment du fait d’optimisations spécifiques au calcul modulaire.

Implémentation naïve de Diffie-Hellman

Je vous propose une implémentation naïve (cliquez sur le bouton Run ▶️ pour l’exécuter) de Diffie-Hellman en Go.

Le premier résultat utilise le groupe multiplicatif du corps $F_{1291799}$ :

---
Diffie-Hellman: F_1291799 multiplicative group
Group order 1291798
Generator 17
---
Amandine generated secret key:
1266948
Amandine transmitted (public) key:
91778
Bastien generated secret key:
81716
Bastien transmitted (public) key:
1089774
Amandine computed shared secret:
489232
Bastien computed shared secret:
489232

Évidemment, ce groupe d’ordre $1291798$ n’est pas à utiliser en pratique.

Je laisse d’ailleurs aux lecteurs et lectrices le soin d’implémenter l’algorithme baby-step giant-step décrit plus haut pour casser le secret ci-dessus…

Notons que les groupes multiplicatifs associés aux corps finis sont le choix d’origine pour l’échange de Diffie-Hellman et qu’ils sont encore utilisés aujourd’hui, avec des groupes dont le paramètre $p$ est sur 2048 bits ou plus.

Utilisation des courbes elliptiques

Qu’est-ce qu’une courbe elliptique ?

L’équation $y^2 = x^3+486662x^2+x$ d’inconnues $x, y$ dans le corps $F_p$ (avec ${p = 2^{255} - 19}$) définit une courbe elliptique sur $F_p$.

Le sujet est bien trop vaste pour une vraie présentation dans le cadre de cet article, remarquons simplement ceci :

• il s’agit d’une courbe plane, son équation relie deux inconnues $x$ et $y$ de la même façon que l’équation ${y - x^2 = 0}$ définit une courbe dans le plan $\R^2$ (en l’occurrence une parabole)
• cette courbe est, comme la parabole, une courbe algébrique : elle est définie par une équation polynomiale à deux indéterminées
• c’est une cubique — le terme dominant de son équation est de degré $3$. La parabole est quant à elle une conique — degré $2$

💡 Parmi les courbes qui ont ces propriétés, les courbes elliptiques ont de plus un genre égal à $1$. Le genre désigne ici une notion de géométrie algébrique qui coïncide dans le cas des courbes complexes avec une notion topologique assez visuelle : les courbes elliptiques sur $\Complex$ ont la même topologie qu’un donut.

Loi de groupe sur les courbes elliptiques

À toute courbe elliptique peut être associée une loi de groupe.

Cette loi est commutative et associe à deux points $P$ et $Q$ de la courbe un troisième point noté $R = P + Q$.

💡 Ébauche de construction

L’idée générale est qu’en considérant deux points situés sur cette courbe, on peut en produire un troisième par un calcul algébrique.

Sans rentrer dans les développements, deux points $P$ et $Q$ d’une courbe plane définissent une droite — l’unique droite qui passe par $P$ et $Q$ (si ${P = Q}$, on considère la droite tangente à la courbe en ce point).

Cette droite admet une équation de la forme $ax + by = c$ où $(a, b) \neq (0, 0)$.

La recherche de tous les points d’intersections de cette droite avec une courbe elliptique amène à résoudre une équation du troisième degré en $x$.

Par exemple pour la courbe définie plus haut : ${(\frac{c - ax}{b})^2 = x^3+486662x^2+x}$

Sous certaines hypothèses supplémentaires (notamment pour prendre en compte le cas $b = 0$ ci-dessus…), on en déduit un mécanisme permettant d’associer aux points $P$ et $Q$ un troisième point $R = P + Q$.

On montre alors que l’opération $+$ ainsi introduite définit une loi de groupe commutatif.

Notons que malgré le vocabulaire de la géométrie plane utilisé ici (droite, tangente), cette construction est purement algébrique et possible sur n’importe quel corps de base — en particulier les corps finis.

💻 Implémentation en Go

Le package elliptic de Go introduit une interface Curve (reproduite ci-dessous) décrivant une courbe elliptique ainsi que différentes implémentations.

type Curve interface {
	// Params returns the parameters for the curve.
	Params() *CurveParams
	// IsOnCurve reports whether the given (x,y) lies on the curve.
	IsOnCurve(x, y *big.Int) bool
	// Add returns the sum of (x1,y1) and (x2,y2)
	Add(x1, y1, x2, y2 *big.Int) (x, y *big.Int)
	// Double returns 2*(x,y)
	Double(x1, y1 *big.Int) (x, y *big.Int)
	// ScalarMult returns k*(Bx,By) where k is a number in big-endian form.
	ScalarMult(x1, y1 *big.Int, k []byte) (x, y *big.Int)
	// ScalarBaseMult returns k*G, where G is the base point of the group
	// and k is an integer in big-endian form.
	ScalarBaseMult(k []byte) (x, y *big.Int)
}

Ce package implémente notamment les courbes P-256 et P-384 recommandées par le NIST et définies sur des corps $F_p$ avec $p$ premier (sur $256$ et $384$ bits respectivement).

Ces courbes sont très utilisées en pratique, bien qu’elles soient l’objet de soupçons de backdoor par la NSA…

Diffie-Hellman avec la courbe P-256

Ci-dessous, voici ce que donne notre implémentation de Diffie-Hellman avec la courbe P-256 (exécuter en ligne) :

---
Diffie Hellman: Elliptic Curve P-256
Field F_115792089210356248762697446949407573530086143415290314195533631308867097853951
Group order 115792089210356248762697446949407573529996955224135760342422259061068512044369
---
Amandine generated secret key:
7342462952232507609821760396776010434242597936110644963427068432176148435477
Amandine transmitted (public) key:
4298064935869640021519201203011003733572235803818690789383769808073692516886
Bastien generated secret key:
110170395102730437573897103177357816686836430099641375606421793187578417842509
Bastien transmitted (public) key:
6169708491757107974945465047131128230446890469460906853603235544851377683418
Amandine computed shared secret:
85470343014045070211971750616744066840724631640773885304746048731416023347568
Bastien computed shared secret:
85470343014045070211971750616744066840724631640773885304746048731416023347568

💡 On remarque que l’ordre du groupe généré est relativement proche de celui du corps fini utilisé : sur leurs $78$ chiffres, les $37$ premiers coincident.
C’est une conséquence d’un théorème connu…

TLS 1.3 et la confidentialité persistante

Avant TLS 1.3, il était possible d’utiliser le même couple de clefs cryptographiques pour l’authentification et l’échange des clefs de session.

Ce mécanisme est qualifié de statique (par exemple static RSA, lorsque l’algorithme sous-jacent est RSA).

Avec TLS 1.3, des clefs asymétriques à usage unique (clefs éphémères) doivent être utilisées pour chaque session.

Ceci permet de garantir une confidentialité persistante : si une clef privée est compromise dans le futur, elle ne pourra pas être utilisée pour déchiffrer a posteriori des communications chiffrées qui auraient été conservées.

Le mécanisme de Diffie-Hellman permet de satisfaire cette exigence, en partageant une clef secrète $S = g^{ab}$ — la clé « pre-master » — basée sur des clefs secrètes $a$ (client) et $b$ (serveur) éphémères.

Les lecteurs et lectrices souhaitant en savoir plus sur le fonctionnement de TLS pourront lire cette présentation par Cloudflare.

Le livre An Introduction to Mathematical Cryptography, utilisé comme source d’inspiration pour cet article, est une référence pour approfondir les notions théoriques.

---

Vous pouvez commenter cette entrée sur Bluesky, Twitter ou Mathstodon.
N'hésitez pas également à m'envoyer un email (thomas@lipsum.dev).

---

• ← Commutativité, Quaternions et WebGL
• Nombres premiers, Miller-Rabin et OpenSSL →