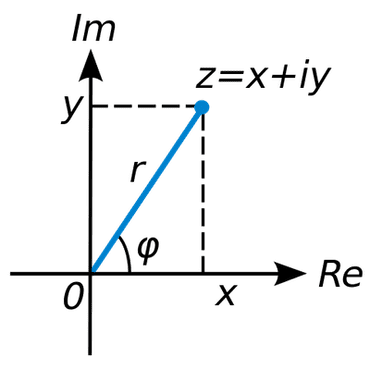Lipsum.dev

Commutativité, Quaternions et WebGL

18 septembre 2020

On peut introduire les nombres complexes de plusieurs façons.

Par exemple, par une approche géométrique, en les associant à des points $(a, b)$ du plan qu’on peut additionner composante par composante.

La multiplication correspond alors à une similitude directe et en particulier les nombres complexes unitaires — sur le cercle unité — correspondent à des rotations.

Une approche algébrique consiste à remarquer que le polynôme réel $X^2 + 1$ est irréductible et permet donc de construire une extension algébrique de degré $2$ des réels — un corps dont les éléments sont des couples de réels.

Cette approche est détaillée dans une entrée précédente.

Ces deux approches sont bien entendu équivalentes – c’est l’art des mathématiques que de faire le lien entre des approches abstraites et des objets plus concrets.

Il n’est pas possible d’utiliser le même procédé pour construire un corps qui soit strictement une extension de $\Complex$ .

Ceci est une conséquence du fait que $\Complex$ est algébriquement clos — nous y reviendrons.

Pourtant, on peut munir l’ensemble des quadruplets $(a, b, c, d)$ de réels d’une multiplication.

L’ensemble obtenu, les quaternions, est presque un corps : il n’est pas commutatif (on peut avoir $x \times y \neq y \times x$ ).

Les quaternions ont un lien subtil avec les rotations de l’espace à trois dimensions et sont utilisés dans de nombreux moteurs 3D.

Le cube ci-dessous utilise par exemple babylon.js, qui repose sur les quaternions pour modéliser les rotations (code source).

Vous pouvez le faire tourner grâce aux flèches directionnelles.

Quaternion : w: —, x: —, y: —, z: —

Nous allons essayer ici de donner une idée de ce que sont ces quaternions, en commençant par quelques rappels sur les nombres complexes.

Des réels aux complexes

Les nombres complexes correspondent au plan $\R^2$ muni d’opérations $+$ et $\times$ avec des propriétés très similaires à celles des nombres réels (qui en font un corps commutatif).

Du point de vue algébrique, on peut les définir comme des nombres de la forme $z = a + bi$ où on a introduit un « nombre » $i$ et les règles de calcul suivantes :

L’addition se fait composante par composante (on somme les parties réelles et imaginaires)
La multiplication est associative et distributive, comme pour les réels, on peut donc calculer le produit de deux complexes en développant les calculs à partir de la table suivante :

×	1	i
1	1	i
i	i	-1

En particulier, la multiplication ainsi définie est commutative.

Tout nombre complexe peut se décomposer sous la forme ${z = r \exp(i\varphi)}$ où $r$ est un réel positif et ${\exp(i\varphi) = \cos(\varphi) + i \sin(\varphi)}$ . Cette forme met en évidence l’interprétation géométrique des nombres complexes :

Les points situés sur le cercle unité (cas $r = 1$ ) correspondent alors à des rotations par un angle $\varphi$ . En particulier, la commutativité de la multiplication des complexes est intrinsèquement liée à la commutativité des rotations du plan.

$\Complex$ est algébriquement clos

Comme expliqué dans une autre entrée, l’existence des nombres complexes est due à l’existence du polynôme réel irréductible $P = X^2 + 1$ , dont on introduit une racine $i$ .

Le corps des nombres complexes est lui algébriquement clos : tout polynôme de degré $n$ y admet $n$ racines comptées avec leur multiplicité.

Ce résultat, connu sous le nom de Théorème fondamental de l’algèbre fut prouvé vers la fin du 18^ème siècle, de façon plus ou moins rigoureuse.

Une de ses conséquences est que tout corps commutatif qui est une extension des complexes est nécessairement de dimension infinie par rapport aux réels : ses éléments ne peuvent pas être décrits par des séquences finies de réels — on parle d’extension transcendante.

En particulier, on ne pourra pas trouver de structure de corps commutatif sur les quadruplets de réels $(a, b, c, d)$ . Comme nous le verrons, il faudra renoncer à la commutativité…

💡 Ébauche d’une preuve

Nous donnons ici un aperçu d’une preuve topologique du théorème fondamental de l’algèbre, cette partie est facultative pour la compréhension de ce qui suit.

Considérons le polynôme $P = X^4 + X^2 + 2X + 10i + 20$ — qui n’a pas de racines réelles, ce dont je vous laisse vous convaincre en considérant par exemple sa partie réelle.

💻 Le code ci-dessous permet d’obtenir l’image d’un cercle centré en l’origine $O$ , de rayon $r$ variant de $R_{max} = 3.2$ à $0$ , par la fonction ${z \to P(z)}$ (on utilise SageMath).

def polynomial(z):
    P = z^4 + z^2 + 2*z + 10*I + 20
    return (P.real(), P.imag())
plots = [
  parametric_plot(polynomial(r*e^(I*x)), (x, 0, 2*pi))
  for r in sxrange(3.2, 0, -0.1)
]
a = animate(plots, xmin=-100, ymin=-150, xmax=200, ymax=150, figsize=[5, 5])
a.show(delay=50)

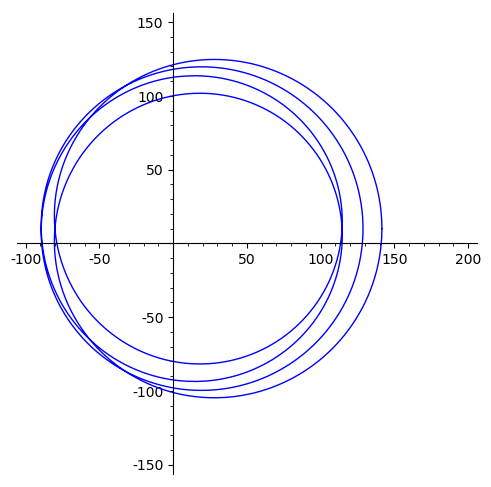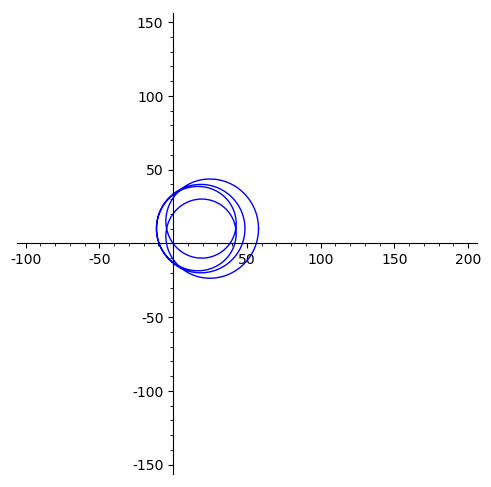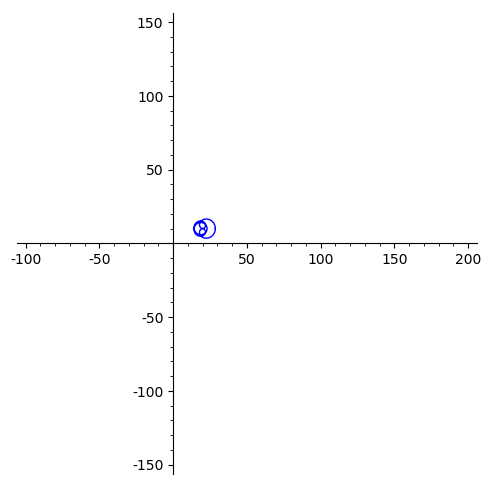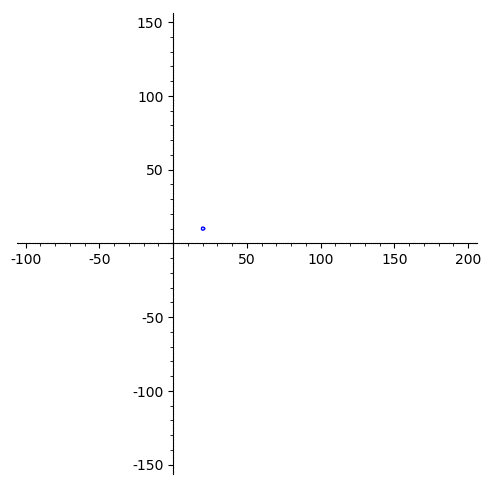
Lorsque $r$ est « grand », le terme dominant $z^4 = r^4 \exp(4i \phi)$ donne une bonne approximation de la courbe obtenue : le cercle unité est transformé en une courbe qui décrit approximativement un cercle de rayon $r^4$ parcouru quatre fois dans le sens trigonométrique.

Lorsque $r$ devient « petit », cette courbe se rétracte pour devenir finalement un simple point correspondant à $P(0)$ , de coordonnées $(20, 10)$ .

La courbe traverse nécessairement l’origine $O$ quatre fois au cours de cette évolution.

L’animation obtenue ci-dessous illustre ainsi cette preuve topologique assez classique.

C est algébriquement clos

Les quaternions

Les quaternions correspondent à la définition de règles de calcul sur l’espace à quatre dimensions $\R^4$ .

Concrètement, on introduit trois « nombres » $i$ , $j$ et $k$ et l’on identifie un point $(a, b, c, d) \in \R^4$ au quaternion $q = a + bi + cj + dk$ .

L’addition se fait composante par composante, comme dans $\Complex$ .
La multiplication est associative et distributive, comme sur $\R$ et $\Complex$ , on peut donc calculer le produit de deux quaternions en développant les calculs à partir de la table suivante :

×	1	i	j	k
1	1	i	j	k
i	i	-1	k	-j
j	j	-k	-1	i
k	k	j	-i	-1

Cette table n’étant pas symétrique, la multiplication n’est pas commutative (par exemple, $i \times j = k$ , différent de $j \times i = -k$ ).

On remarque en particulier que les règles de calcul sur les deux premières composantes (terme réel et terme « en $i$ ») sont identiques à celles de $\Complex$ : les quaternions sont une extension des complexes.

Exercice : En utilisant les règles ci-dessous, déterminer les quatres coefficients du produit $(a + bi + cj + dk) \times (a' + b'i + c'j + d'k)$ .
On pourra vérifier le résultat en comparant avec l’implémentation de la multiplication des quaternions dans babylon.js.

Norme d’un quaternion

De façon analogue aux nombres complexes, on définit le conjugué de $q$ , ${\bar{q} = a - bi - cj - dk}$ , et je vous laisse vérifier l’égalité : ${q\bar{q} = a^2 + b^2 + c^2 + d^2}$

On définit également la norme ${\vert q \vert = \sqrt{q\bar{q}} = \sqrt{a^2 + b^2 + c^2 + d^2}}$

La norme des quaternions est multiplicative : $\vert q_1 q_2 \vert = \vert q_1 \vert \vert q_2 \vert$ .

Si $q$ est un quaternion non nul, on a alors ${\cfrac{q \bar{q}}{{\vert q \vert}^2} = 1}$ , ce qui permet de définir l’inverse de $q$ , de façon analogue aux nombres complexes : ${q^{-1} = \cfrac{\bar{q}}{{\vert q \vert}^2}}$ .

Rotations dans l’espace

On appelle rotation une transformation de l’espace qui préserve l’origine $O$ , la distance (euclidienne) entre les points et l’orientation. L’ensemble des rotations de l’espace à trois dimensions est noté $SO(3)$ .

De façon plus intuitive, elles correspondent aux transformations qui font tourner un objet autour d’un point central sans le déformer.

Les rotations de l’espace à trois dimensions correspondent à la donnée d’un axe de rotation et d’un angle.

Par exemple, la rotation associée à la flèche de gauche $\boxed{\leftarrow}$ dans l’animation du cube correspond à une rotation de $-\frac{\pi}{2}$ autour de l’axe qui pointe vers le haut.

Cette caractérisation des rotations est aujourd’hui bien connue, mais elle n’est pas évidente a priori. Euler l’a prouvée en 1776 par des arguments de géométrie sphérique.

Aujourd’hui, le formalisme de l’algèbre linéaire permet d’aboutir à ce résultat par un calcul plus concis.

Ces deux preuves sont détaillées dans l’article Wikipedia consacré.

Non commutativité des rotations dans l’espace

Considérons le cube présenté en introduction — mais vous pouvez aussi faire l’expérience plus concrètement, par exemple en manipulant un dé à jouer.

Notons $L$ , $R$ , $U$ , $D$ (Left, Right, Up, Down) les rotations accessibles dans l’animation.

Elles correspondent à des rotations d’un quart de tour autour de l’axe vertical (Left et Right) ou de l’axe horizontal de votre écran (Up et Down).

On peut effectuer ces opérations successivement, et l’on notera par exemple ${L \cdot U \cdot R}$ l’application successives des opérations $R$ , puis $U$ , puis $L$ .

Notons également $I$ la transformation identité, qui laisse le cube dans son état d’origine.

On remarque alors que ${U \cdot D = I}$ et ${L \cdot R = I}$ , mais ${U \cdot L \cdot D \cdot R \neq I}$ : la séquence Haut, Gauche, Bas, Droite ne ramène pas le cube dans sa configuration d’origine.

Le phénomène mis en évidence est la non commutativité des rotations dans l’espace, lorsque les axes de rotation ne sont pas confondus.

Rotations et quaternions

Une rotation peut être décrite par un axe de rotation donné par un vecteur directeur unitaire $\overrightarrow{u}$ , et un angle $\theta$ .

$\overrightarrow{u}$ est lui-même défini par ses trois coordonnées $(x,y,z)$ vérifiant ${x^2 + y^2 + z^2 = 1}$ .

Il est possible d’encoder l’ensemble de ces informations dans un quaternions de la façon suivante :

${q = \cos(\frac{\theta}{2}) + \sin(\frac{\theta}{2})(xi + yj + zk)}$

On remarque que les quaternions associés à des rotations de cette façon sont unitaires :

{\vert q \vert}^2 = (\cos(\tfrac{\theta}{2}))^2 + (\sin(\tfrac{\theta}{2}))^2 (x^2 + y^2 + z^2) \\ = (\cos(\tfrac{\theta}{2}))^2 + (\sin(\tfrac{\theta}{2}))^2 \\ = 1

Les coefficients d’un tel quaternion définissent de façon unique une rotation.

En revanche, la même rotation est décrite par deux quaternions unitaires différents. Par exemple, la rotation identité — qui laisse les objets dans la même position — peut être décrite par les quaternions suivant :

$q_0 = (1, 0, 0, 0)$ , en prenant $\theta = 0$
$q_1 = (-1, 0, 0, 0)$ , en prenant $\theta = 2\pi$

On peut le constater en faisant faire un tour complet au cube présenté en introduction depuis sa position d’origine décrite par le quaternion $q_0$ .

Après une séquence ${\boxed{\leftarrow}, \boxed{\leftarrow}, \boxed{\leftarrow}, \boxed{\leftarrow}}$ les coordonnées du quaternion correspondant — affichées sous le cube – sont différentes et correspondent à $q_1$ .

On peut effectuer un autre tour dans le même sens pour retrouver le quaternion initial $q_0$ .

On peut encoder les rotations de l’espace à trois dimensions en utilisant des quaternions unitaires.
À toute rotation de l’espace correspond alors deux quaternions unitaires qui la décrivent.

Le produit des quaternions est compatible avec la composition des rotations : si $q$ et $q'$ sont deux quaternions unitaires représentant des rotations, le quaternion $q' q$ représente l’application successive de ces deux rotations.

Dès lors, on peut déjà rapprocher la non-commutativité du produit des quaternions et la non commutativité des rotations de l’espace…

On montre par ailleurs que si l’on encode un vecteur $(a, b, c)$ de l’espace à trois dimensions sous la forme d’un quaternion $p = ai + bj +ck$ , alors le produit $qpq^{-1}$ donne le résultat de l’application de la rotation associée à $q$ au vecteur représenté par $p$ .

💻 Utilisation des quaternions

Les quaternions sont utilisés dans la plupart des moteurs 3D afin de représenter la rotation d’un solide par rapport à un repère initial.

Par exemple, les frameworks babylon.js et three.js, qui permettent de faire de la 3D dans la navigateur en utilisant le standard WebGL se basent sur des quaternions pour leur représentation interne des rotations.

L’API de babylon.js permet de spécifier une rotation par son axe et son angle, ou par les angles d’Euler — qui permettent de définir un repère en mouvement avec le solide.

Quelle que soit la méthode utilisée, la représentation interne reste cependant un quaternion.

Le moteur de jeux vidéos Unity cite les avantages suivant pour l’utilisation des quaternions (source) :

They are compact, don’t suffer from gimbal lock and can easily be interpolated. Unity internally uses Quaternions to represent all rotations.

La compacité de la représentation est principalement liée au fait que seuls quatre flottants soient nécessaires pour représenter une rotation. Plus de détails sur la comparaison des opérations de rotation dans les différentes représentations sont donnés dans l’article Wikipedia à ce sujet.

Blocage de cardan

Le problème du blocage de cardan (gimbal lock) correspond à l’observation suivante :

autour d’une position donnée, un solide peut effectuer des rotations selon trois degrés de liberté, qui correspondent à des rotations autour de chacun des trois axes
certaines représentations, comme celle associée aux angles d’Euler, amènent parfois le solide dans un état où un degré de liberté est perdu : lorsque deux axes de rotation coincident

La représentation par les quaternions unitaires ne présente pas ce problème.

Interpolation d’une rotation

Comment passer d’une rotation à une autre de façon continue, en parcourant une distance minimale ?

Cette problématique correspond à ce que l’on appelle l’interpolation linéaire sphérique (ou Slerp) et se pose dans les moteurs 3D pour générer une animation entre deux rotations différentes.

Si les deux rotations sont spécifiées par des quaternions $q_0$ et $q_1$ , il est possible de le faire en considérant pour ${0 \leq t \leq 1}$ le quaternion ${q_0(q_0^{-1}q_1)^t}$ .

Cette formule nécessite d’avoir défini une notion d’exponentielle, qui généralise l’exponentielle réelle ou complexe et dont la justification nécessite l’étude des groupes et algèbres de Lie, que nous évoquerons brièvement.

Dans l’animation du cube, nous utilisons la méthode Quaternion.Slerp pour générer les transitions entre les différentes rotations.

💡 Le revêtement double de $SO(3)$

La suite de cette entrée, plus avancée, vise à donner un éclairage sur l’origine des quaternions et leur lien avec les rotations de l’espace.

Dimension de $SO(n)$

Dans un espace de dimension $n$ avec une base orthonormée fixée, les isométries qui fixent l’origine sont décrites par des matrices orthogonales, qui forment un ensemble noté $O(n)$ .

La relation $MM^{\intercal} = I$ est symétrique. Elle correspond à $n(n+1)/2$ équations qui sont autant de contraintes sur les coefficients de $M$ .

L’ensemble des matrices obtenues constitue donc une variété (au sens de la géométrie différentielle) de dimension $n^2 - n(n+1)/2 = {n(n-1)}/2$ .

Ces transformations ont un déterminant égal à $1$ ou $-1$ suivant qu’elles conservent ou inversent l’orientation. Le groupe $SO(n)$ des rotations correspond au cas $\det(M) = 1$ .

On a par exemple $I \in SO(n)$ et l’on peut paramétrer localement $SO(n)$ à l’aide de ${n(n-1)}/2$ variables.

On dit que $SO(n)$ est un groupe de Lie de dimension $\cfrac{n(n-1)}{2}$ .

Cas $n = 2$

On a alors $\cfrac{n(n-1)}{2} = 1$ .

L’ensemble $SO(2)$ des rotations du plan et le cercle unité $S^1$ (notation de la 1-sphere) ont même dimension. On montre même qu’ils sont homéomorphes, ce que l’on notera ${S^1 \simeq SO(2)}$ .

C’est cette identification qui nous permet de munir $\R^2 \simeq \R^+ \times S^1 \simeq \R^+ \times SO(2)$ de la multiplication complexe.

Cas $n = 3$

On a alors $\cfrac{n(n-1)}{2} = 3$ .

L’ensemble $SO(3)$ des rotations de l’espace forme une variété de dimension $3$ (c’est par exemple pour cela qu’il y a trois angles d’Euler).

La sphère $S^3$ de l’espace à quatre dimensions est également une variété de dimension $3$ qui correspond aux quaternions unitaires.

En encodant une rotation dans un quaternion unitaire, on obtient la correspondance ${S^3 \simeq SO(3) \times \{-1, 1\}}$ . Les points de $S^3$ forment du point de vue topologique un revêtement double de l’ensemble des rotations de l’espace.

On a alors l’identification $\R^4 \simeq \R^+ \times S^3 \simeq \R^+ \times SO(3) \times \{-1, 1\}$ .

C’est cette identification qui nous permet de munir $\R^4$ d’un produit pour construire les quaternions.

Elle met en évidence le lien avec les rotations de l’espace à trois dimensions, qui est plus subtil que le lien entre les complexes et les rotations du plan…

Rotations et revêtements

On peut voir les rotations du plan et de l’espace comme des structures définies par des quotients d’un groupe de Lie par un sous-ensemble qui possède une forme de régularité (techniquement, un sous-groupe discret).

SO(2) \simeq \R / {2\pi\Z} \\ SO(3) \simeq S^3 / \{-1, 1\}

Les groupes de rotations $SO(2)$ et $SO(3)$ apparaissent alors comme les images d’ensembles plus grands dont on aurait « oublié » des informations.

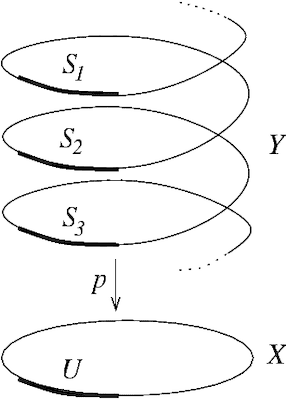
L’application $t \to \exp(it)$ définit par exemple un revêtement du cercle unité (ou de $SO(2)$ ) par $\R$ , comme l’illustre la figure ci-dessous :

Dans ce cas, ce revêtement fait apparaître l’infinité de réels décrivant une rotation donnée.

Concernant $SO(3)$ , on a un revêtement par les quaternions unitaires et ce revêtement possède une propriété commune avec celui du cercle par les réels : c’est un revêtement par un espace simplement connexe.

La subtilité est que dans ce cas une rotation n’est pas décrite par une infinité de quaternions unitaires, mais seulement par deux. Le passage de $S^3$ à $SO(3)$ correspond en effet à identifier les points antipodaux.

Une bonne compréhension de ces notions demande de s’intéresser à la notion d’algèbre de Lie associée à un groupe de Lie.

Le groupe des quaternions unitaires apparaît alors comme un cas particulier de groupe de Lie, qui partage avec $SO(3)$ la même algèbre de Lie. Il s’agit de son revêtement universel…

Maths et applications, avec les mains et avec du code 💻
Suivre sur Twitter