Histoires de surfaces, de Gauss à OpenStreetMap

28 août 2020

Si vous prenez un lacet de longueur $L$ dans vos mains, vous êtes libre de le déformer sans l’étirer — sans jouer sur son élasticité.

Vous pouvez par exemple le disposer le long d’un cercle de circonférence $L$ ou d’une forme plus compliquée comme ci-dessous (source) :

Ce lacet correspond à ce que l’on appelle mathématiquement une variété de dimension $1$ — une seule coordonnée permet de s’y repérer — et une déformation sans étirement est ce que l’on appelle une isométrie.

Les surfaces que nous allons étudier ici, sont des variétés de dimension $2$.

De façon assez surprenante, un phénomène se produit à partir de la dimension $2$ puisqu’il existe une courbure intrinsèque, qui restreint les possibilités de déformation isométrique.

Je vous propose ici une petite présentation du formalisme des surfaces, tel qu’introduit par Gauss au début du XIX^ème sièce, et dont l’un des résultats est le Theorema Egregium (théorème remarquable), qui formalise cette notion de courbure intrinsèque.

Cette étude permet aussi de comprendre certaines problématiques de cartographie, qui ont des conséquences très concrètes sur la manipulation des données géographiques en informatique.

Elle permet également de comprendre pourquoi les plis des vêtements sont inévitables.

Enfin, le formalisme adopté ici constitue les prémices de la géométrie Riemanienne, utilisée notamment pour décrire l’espace-temps de la relativité générale.

Les prérequis pour comprendre cette entrée sont d’être à l’aise avec la notion de dérivée partielle et d’avoir quelques notions sur les matrices.

Surfaces lisses

Nous allons ici nous intéresser à ce qu’on appelle mathématiquement des surfaces paramétrées.

Ces surfaces peuvent localement — c’est-à-dire au voisinage de chaque point $M$ — être décrites de façon bijective par deux variables $(u, v)$ qui paramètrent leurs coordonnées $(x, y, z) = \Phi(u, v)$.
On dit que $\Phi$ est une carte locale autour de $M$.

On parlera ici de surfaces lisses (ou $C^{\infty}$), où la fonction $\Phi$ est infiniment dérivable par rapport à chaque variable.

On considérera uniquement des surfaces régulières : en tout point $M$ et pour toute carte locale $\Phi$, les vecteurs $\cfrac{\partial{\Phi}}{\partial{u}}(M)$ et $\cfrac{\partial{\Phi}}{\partial{v}}(M)$ sont linéairement indépendants (ceci permettra de définir le plan tangent).

Plan tangent

Si l’on considère une fonction numérique (de $\R$ dans $\R$), la dérivée $f'(x_0)$ permet de déterminer la droite tangente à la courbe $y = f(x)$ autour du point $x_0$, qui est la droite à laquelle la courbe ressemble au voisinage de $x_0$.

Dans le cas d’une surface $S$, on va chercher à l’approximer localement par un plan : le plan tangent.

C’est le plan passant par $M$ et dirigé par les deux vecteurs $\cfrac{\partial{\Phi}}{\partial{u}}(M)$ et $\cfrac{\partial{\Phi}}{\partial{v}}(M)$.

Métrique

La notion de métrique va permettre de mesurer les longueurs parcourues le long des courbes.

Considérons un point $M(t)$ se déplaçant dans l’espace de façon lisse entre les temps $t = 0$ et $t = 1$. La vitesse instantanée du point au temps $t$ est $\cfrac{dM}{dt}(t)$ et l’on obtient la longueur de l’arc (c’est-à-dire la distance parcourue par le point) par intégration : $\ell = \int_{0}^{1}{\Vert\frac{dM}{dt}(t)\Vert dt}$

On utilise ici la norme euclidienne ${\Vert V \Vert = \sqrt{{v_x}^2 + {v_y}^2 + {v_z}^2}}$ définie dans l’espace ambiant $\R^3$.

Si l’on contraint le point $M$ à évoluer le long de la surface $S$, alors on peut écrire $M(t) = \Phi(u(t), v(t))$.

On obtient alors une décomposition du vecteur vitesse instantanée dans le plan tangent à tout instant : $\cfrac{dM}{dt}(t) = \cfrac{\partial{\Phi}}{\partial{u}}(u(t), v(t)) \cfrac{du}{dt}(t) + \cfrac{\partial{\Phi}}{\partial{v}}(u(t), v(t)) \cfrac{dv}{dt}(t)$

D’où l’on déduit en particulier : ${\Vert\cfrac{dM}{dt}\Vert}^2 = E {\cfrac{du}{dt}}^2 + 2F {\cfrac{du}{dt}{\cfrac{dv}{dt}} + G{\cfrac{dv}{dt}}^2}$

En notant $E$, $F$ et $G$ les coefficients qui interviennent dans cette expression et qui s’expriment à partir des dérivées partielles de $\Phi$.

On désigne généralement par $s(t)$ l’abscisse curviligne mesurée le long de la courbe décrite par $M(t)$.

On peut alors réécrire l’égalité précédente sous la forme ${{ds}^2 = E{du}^2 + 2F{du}{dv} + G{dv}^2}$.

Mathématiquement, cette notation a un sens dans le cadre des formes différentielles.

Nous l’interpréterons cependant avec un langage approximatif assez courant : l’élément de longueur $ds$ correspondant à un petit changement de coordonnées $(du, dv)$ s’exprime par l’expression ci-dessus en fonction de $du$ et $dv$.

Cette expression, qui définit la métrique de la surface, est ce que l’on appelle une forme quadratique, souvent présentée sous forme matricielle :

Ces trois coefficients ont été introduits par Gauss avec ces mêmes notations, et définissent ce que l’on appelle la première forme fondamentale de la surface au point $M$.

Remarquons en particulier que dans le cas d’une surface plane munie d’un repère orthonormé, un déplacement infinitésimal $(dx, dy)$ correspond à une distance parcourue $ds$ donnée par ${{ds}^2 = {dx}^2 + {dy}^2}$ (théorème de Pythagore). C’est un cas particulier où $E = G = 1$ et $F = 0$ (la matrice correspondante est l’identité).

La connaissance de cette forme permet de calculer la longueur des arcs tracés sur la surface, en « sommant les $ds$ » le long du trajet.

Étude de la sphère

La sphère unité est définie par l’équation $x^2 + y^2 + z^2 = 1$. On peut la paramétrer à l’aide de deux angles $\lambda \in ]-\pi, \pi[$ (longitude) et $\phi \in ]-\frac{\pi}{2}, \frac{\pi}{2}[$ (latitude) comme sur la figure ci-dessous.

Avec un choix d’axes approprié, on a les correspondances suivantes (voir coordonnées sphériques) :

Je laisse le lecteur en déduire en exercice :

${{ds}^2 = {\cos(\phi)}^2 {d\lambda}^2 + {d\phi}^2}$

c’est-à-dire :

Une première carte terrestre

Voici ci-dessous ce que l’on obtient si l’on considère que la Terre est sphérique et que l’on utilise la latitude et la longitude introduites ci-dessus pour tracer une carte.

Cette représentation, connue notamment sous le nom de plate-carrée a été introduite autour du premier siècle de notre ère. Elle est cependant très peu utilisée du fait de certains défauts que nous allons voir ci-dessous.

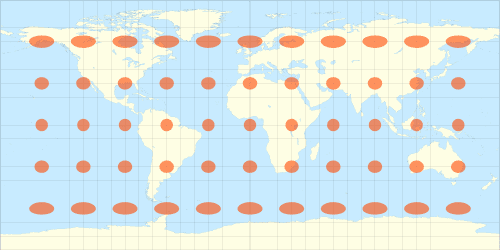
Indicatrice de Tissot

L’indicatrice de Tissot est une représentation permettant d’indiquer la distorsion associée à une représentation de la Terre.

L’idée est de tracer des disques de mêmes rayons sur la surface de la Terre, et d’observer comment ils sont représentés dans une carte donnée. La distorsion induite par la représentation cartographique transforme approximativement ces disques en des ellipses dont la visualisation permet de saisir rapidement les défauts de la carte.

Sur l’exemple ci-dessus, l’indicatrice de Tissot peut être interprétée à l’aide des coefficients $E$, $F$ et $G$  :

• L’absence de distorsion verticale des ellipses obtenues traduit l’égalité $G = 1$ et signifie que l’on peut mesurer les trajets verticaux (axe Nord-Sud) de façon correcte sur cette carte (on parle parfois de carte « équidistante », mais cela peut prêter à confusion car ce n’est que selon cet axe).
• La distorsion horizontale, d’autant plus marquée lorsque l’on se rapproche des pôles, traduit la dépendance du paramètre $E$ par rapport à la latitude.
• Comme $F = 0$, les deux axes des ellipses correspondent bien aux axes horizontaux et verticaux. Le système de coordoonnées $(\lambda, \phi)$ est orthogonal.

Je vous renvoie à cet article pour d’autres exemples de cartes avec leurs indicatrices de Tissot.

Cartes conformes

Le fait que les indicatrices de Tissot soient déformées — les cercles donnent des ellipses — est problématique : la carte n’est pas conforme, elle ne préserve pas la forme des petits objets.

Un système de coordonnées est conforme, si sa première forme fondamentale vérifie les conditions suivantes : $F = 0$ et $E = G$.

La matrice correspondante est donc égale à un multiple de la matrice identité, le facteur $E = G$ pouvant varier d’un point à l’autre de la surface.

Intuitivement, avec une représentation conforme le facteur d’échelle ou de dilatation est le même dans toutes les directions.

Si l’on considère l’indicatrice de Tissot développée plus haut, les cartes conformes ont des indicatrices qui sont des cercles.

On montre que cette notion de transformation conforme revient à exiger que tous les angles d’intersection entre les courbes soient conservés.

Surfaces de révolution

En faisant tourner une courbe d’équation $y = f(x)$ (la courbe directrice) autour de l’axe $Ox$ dans l’espace à trois dimensions, on obtient une surface de révolution.

Ci-dessous, voici une surface obtenue à partir d’une courbe directrice d’équation $y = 2 + \sin(x \ln(x))$ (en rouge) :

Exercice : La sphère peut aussi s’obtenir comme une surface de révolution. Quelle équation de courbe $y = f(x)$ utiliseriez-vous pour la générer ?
💻 Vous pourrez vérifier le tracé en utilisant la fonction revolution_plot3d de SageMath.

Représentation conforme d’une surface de révolution

Une surface de révolution peut être paramétrée par les deux variables définies ci-dessous :

• L’angle de rotation $\lambda$ autour de l’axe de révolution.
• L’abscisse curviligne $t$ le long de la génératrice. Cette variable mesure la distance parcourue lorsque l’on se déplace le long d’une génératrice de la surface, en maintenant donc un angle $\lambda$ constant.

Notons que nous avons en fait déjà utilisé ces coordonnées plus haut, dans le cas de la sphère unité. L’angle $\lambda$ correspond alors à la longitude et l’abscisse curviligne $t$ le long d’un demi-cercle générateur correspond à la latitude $\phi$, l’origine étant prise sur l’équateur.

Nous allons essayer d’obtenir un paramétrage conforme qui utilise la variable de longitude $\lambda$ mais qui remplace $t$ par une autre variable $\alpha$, qui lui correspond de façon bijective.

On a alors une relation du type $u = \alpha(t)$ et l’on cherchera une transformation qui vérifie $\alpha'(t) > 0$.

La métrique s’exprime simplement dans le système de coordonnées $(\lambda, t)$ car il est orthogonal et équidistant vis-à-vis de $t$ par définition d’une abscisse curviligne :

${ds}^2 = {dt}^2 + {r(t)}^2 {d\lambda}^2$ en notant $r(t)$ la distance d’un point $(\lambda, t)$ par rapport à l’axe de révolution

Le changement de coordonnées donnant $du = \alpha'(t) dt = \alpha'(\alpha^{-1}(u)) dt$, on peut exprimer la métrique dans le système $(\lambda, u)$ :

${ds}^2 = \cfrac{{du}^2}{{\alpha'(\alpha^{-1}(u))}^2} + {r(\alpha^{-1}(u))}^2 {d\lambda}^2$

La condition pour que ce système soit conforme est donc ${\cfrac{1}{\alpha'(\alpha^{-1}(u))} = r(\alpha^{-1}(u))}$, ce qui se réécrit en fonction de $t$ : ${\alpha'(t) = \cfrac{1}{r(t)}}$.

Il est donc toujours possible de paramétrer une surface de ce type par un système de coordonées conforme $(\lambda, u)$ et l’on obtient $u$ par intégration de la formule précédente, ce qui donne $u(t_0) = \int_0^{t_0}{\frac{dt}{r(t)}}$.

Selon les cas, on pourra ou non donner une expression plus simple à cette intégrale.

La projection de Mercator correspond au cas de la sphère, que nous étudions ci-dessous.

La projection de Mercator

Dans le cas de la sphère paramétrée par la latitude et la longitude (notée $\phi$ par convention, car c’est un angle, et non pas $t$), on a $r(\phi) = \cos(\phi)$.

On obtient alors l’expression suivante : ${u(\phi) = \ln(\tan(\frac{\pi}{4} + \frac{\phi}{2}))}$ (je vous laisse vérifier que cette fonction convient…).

En utilisant cette coordonnée verticale pour tracer une carte du monde, on obtient la projection de Mercator.

Cette projection fut introduite au cours du 16^ème siècle, mais le formalisme mathématique permettant de justifier la formule ci-dessus est plus récent (voir Wikipedia). Elle est tronquée au Nord et au Sud, sinon elle s’étendrait verticalement à l’infini.

Déformation des aires

On vérifie visuellement à l’aide de l’indicatrice de Tissot ci-dessus que la carte est bien conforme, les indicatrices ont une forme circulaire.

En revanche, certains de ces disques sont plus gros que d’autres : la carte ne conserve pas les aires, on dit qu’elle n’est pas équivalente.

Le facteur d’échelle local peut se calculer à partir du déterminant de la matrice de la première forme fondamentale :

Dans le cas de la projection de Mercator, on obtient un facteur d’échelle égal à $\cfrac{1}{\cos(\phi)}$.

Les distances sur la carte sont multipliées par ce facteur par rapport à la réalité, ce qui explique que les pays situés plus près des pôles apparaissent plus grand qu’ils ne le sont réellement.

Si l’on souhaite avoir une représentation $(u, v)$ conforme ($F = 0$ et $E = G$) et équivalente ($EG - F^2 = \text{constante}$), il faut que la métrique soit de la forme ${ds}^2 = E({du}^2 + {dv}^2)$ avec un coefficient $E$ constant.

En divisant les coordonnées par $\sqrt{E}$ on obtient alors une carte isométrique : toutes les distances sont conservées.

Le Theorema Egregium nous montrera qu’il est impossible de concevoir une telle carte plane…

Carte équivalente

Si l’on renonce à avoir une carte conforme, on peut alors avoir une carte équivalente (qui conserve les aires). Le raisonnement est le même que celui que l’on a fait pour obtenir l’équation différentielle menant à une représentation conforme des surfaces de révolution.

On utilise comme paramètre la longitude $\lambda$ et un second paramètre $v$ à déterminer en fonction de $t$, de façon à avoir un déterminant $EG - F^2$ constant.

Exercice : Déterminer l’équation différentielle vérifiée par $v$ pour obtenir une représentation équivalente puis montrer que dans le cas de la sphère unité le paramètre $v = \sin(\lambda)$ convient.

La carte ainsi obtenue est la projection cylindrique équivalente de Lambert, elle rend compte de la taille réelle des continents mais pas de leur forme.

💻 Traitement informatisé

Le traitement informatique des données géographiques est un sujet assez vaste dont nous ne donnons ici qu’un aperçu sommaire, en particulier sur deux aspects.

Système géodétique WGS 84

WGS 84 est un système géodétique, il permet de modéliser la Terre et de définir un référentiel commun de coordonnées (latitude, longitude).

Il définit notamment :

• un ellipsoïde de référence modélisant la Terre, et un référentiel commun pour les coordonnées (latitude, longitude)
• un géoïde de référence, qui est une surface équipotentielle du champ de pesanteur — qui est donc perpendiculaire à cette surface, ce qui est utile pour certaines mesures

Ce système tient donc compte du fait que la Terre n’est pas parfaitement ronde. Elle reste cependant modélisée par une surface de révolution et on a vu plus haut qu’on peut en obtenir une représentation conforme.

Ce système est notamment utilisé pour les applications suivantes :

• Positionnement GPS

• Système de coordonnées par défaut dans PostGIS, l’extension géographique de PostgreSQL. La requête ci-dessous nous donne par exemple la distance en mètres entre Paris et Rome (SRID=4326 correspond au système de coordonnées WGS 84) :

SELECT ST_DistanceSphere(
    ST_GeometryFromText('POINT(2.3522 48.8566)', 4326),     -- Paris
    ST_GeometryFromText('POINT(12.4964 41.9028)', 4326)     -- Roma
);
st_distancesphere 
-------------------
  1105281.67043299

• Coordonnées affichées dans la plupart des logiciels de cartographie (OpenStreetMap, Google Maps, Bing, etc.)

La projection Web Mercator

Voici une carte interactive fournie par OpenStreetMap.

Cette carte utilise un moteur open-source en Javascript, Leaflet, les tuiles (tiles — images formant la texture de la carte) étant fournies par OpenStreetMap.

Le système de projection utilisé, introduit par Google en 2005, s’intitule Web Mercator et est très proche de la projection de Mercator étudiée précédemment, à la différence que :

• Web Mercator utilise le système de coordonnées WGS 84, correspondant à une représentation ellipsoïdale de la Terre
• Cependant, la projection est effectuée avec les formules de projection sphérique (celles que nous avons calculées plus haut pour une sphère unité)

Cette subtilité induit une très légère distorsion de la carte obtenue — qui n’est pas exactement conforme — mais permet un gain en rapidité.

La différence de complexité entre les deux modes de projection peut se constater en examinant les implémentations fournies par Leaftlet pour la projection sphérique et la projection ellipsoïdale.

Theorema Egregium

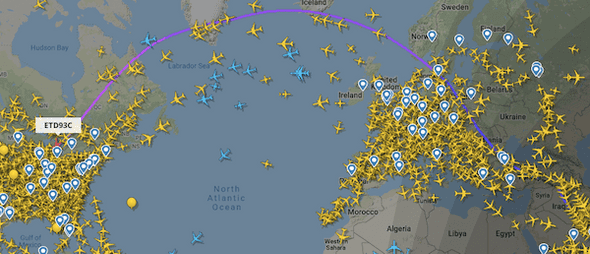
Le site Flight Radar 24 permet de visualiser la trajectoire des avions.

En voici un exemple pour un vol Abu Dhabi - Chicago :

Comme on peut le constater, la trajectoire empruntée ne correspond pas vraiment à une ligne droite sur la carte utilisée (projection de Mercator).

Cela traduit le fait que la notion de « plus court chemin » ne se transpose pas toujours entre deux surfaces en correspondance via une représentation, même conforme.

Pour que les distances soient conservées entre tous les couples de points d’une surface $S$ et leurs représentations par une carte $\phi(u, v)$, il faut en particulier que ce soit vrai pour des points très proches, ce qui correspond à une première forme fondamentale décrite par la matrice identité : ${{ds}^2 = {du}^2 + {dv}^2}$ (cas d’une isométrie locale).

Nous allons voir qu’une telle isométrie n’existe pas entre une surface sphérique et une surface plane…

Courbure de Gauss

La courbure de Gauss d’une surface peut être définie de plusieurs façons équivalentes.

L’une d’entre elles est d’utiliser la représentation ci-dessous :

En tout point $M$ de $S$, on peut définir un vecteur normal unitaire à partir des vecteurs de base du plan tangent $\cfrac{\partial{\Phi}}{\partial{u}}(M)$ et $\cfrac{\partial{\Phi}}{\partial{v}}(M)$.

L’étude de la façon dont ce vecteur varie au voisinage de $M$ est encodée dans ce que l’on appelle la seconde forme fondamentale de la surface, à laquelle on peut associer une matrice.

L’étude de cette matrice montre l’existence de deux plans orthogonaux dont l’intersection contient la normale en $M$ et tels que la courbe décrite par l’intersection de ces plans avec la surface $S$ ait dans l’un une courbure maximale $k_{max}$ et dans l’autre une courbure minimale $k_{min}$.

Le produit $K = k_{min} k_{max}$ de ces deux courbures définit la courbure de Gauss.

Exemples :

• Dans le cas du plan, on a $k_{min} = k_{max} = 0$ et donc $K = 0$ en tout point
• Dans le cas d’un cylindre vertical de rayon $R$, on a $k_{min} = 0$ (plan vertical) et $k_{max} = \frac{1}{R}$ (plan horizontal) donc $K = 0$ également
• Dans le cas d’une sphère de rayon $R$, on a $k_{min} = k_{max} = \frac{1}{R}$ donc $K = \frac{1}{R^2}$
• Pour le point-selle illustré plus haut, la courbure est négative (les deux cercles tangents sont de part et d’autre de la surface)

Theorema Egregium (Théorème remarquable)

Dans son étude Disquisitiones generales circa superficies curvas Gauss écrivait en 1827 :

…e solis quantitatibus $E$, $F$, $G$ atque earum quotientibus differentialibus primi et secundi ordinis…

L’expression de la courbure $K$ ne dépend que des coefficients de la métrique ($E$, $F$, $G$) et de leurs dérivées premières et secondes.

Nous ne faisons pas la démonstration de ce résultat, elle demande des calculs plus complexes que les précédents.

Conséquences

En d’autres termes, la courbure $K$ est invariante par isométrie : si $M$ est envoyé sur $M'$ par une isométrie alors $K(M) = K(M')$.

Deux surfaces entre lesquelles on peut espérer trouver une isométrie doivent donc a minima avoir la même courbure de Gauss aux points correspondants, ce qui exclut le cas d’une représentation à l’échelle de la sphère sur un plan (même partiellement).

En revanche, cela n’interdit pas de trouver une isométrie entre une surface plane et un cylindre, et c’est ce que nous effectuons en pratique lorsque nous déroulons un papier cadeau de son tube…

Pour aller plus loin

Les surfaces telles que nous les avons définies ici sont un cas particulier de variétés Riemaniennes.

La géométrie Riemanienne rend le concept de métrique plus abstrait en étudiant des variétés qui ne sont pas définies à partir d’un espace ambiant : on peut par exemple définir des surfaces qui ne sont pas représentables dans notre espace à trois dimensions.

Elles se définissent en toute dimension, l’expression de la métrique $ds$ à l’aide des coefficients $E$, $F$ et $G$ se généralise ainsi avec la notion de tenseur métrique.

On montre alors que les isométries locales préservent un invariant qui est le tenseur de courbure (ou tenseur de Riemann), généralisant le Theorema Egregium.

La description de ce tenseur, plus complexe que la courbure de Gauss, met en évidence des phénomènes propres aux dimensions $3$, $4$ et supérieures dont l’étude permet par exemple de comprendre certaines manifestations des ondes gravitationnelles.

Les lecteurs et lectrices désirant aller plus loin pourront lire le livre Initiation à la géométrie de Riemann, qui a servi de source d’inspiration pour les calculs développés ici.

Maths et applications, avec les mains et avec du code 💻
Suivre sur Twitter

• ← Polynômes, extensions de corps et QR codes
• Commutativité, Quaternions et WebGL →