Arithmétique modulaire, RSA et clefs privées
27 avril 2020 — Cryptographie, Python
L’arithmétique modulaire correspond aux calculs effectués « à un multiple de n près ».
Par exemple, si on calcule modulo , on a et .
Ce cas particulier correspond à des calculs sur des nombres d’heures, le résultat s’affichant sur un cadran d’horloge ne permettant de connaître l’heure qu’à un multiple de heures près.
Pour ramener des calculs d’un ensemble plus grand (ici les entiers relatifs ) à un ensemble plus petit (ici ), les mathématiciens utilisent la notion d’ensemble quotient.
Nous utiliserons ici cette approche, sur le cas particulier des ensembles (définis pour tout entier ), qui sont le cadre naturel de l’arithmétique modulaire.
Ces ensembles, qui contiennent éléments, seront très utiles en informatique. Leurs éléments peuvent tous être représentés avec un espace mémoire fini (contrairement à ) et les calculs y sont exacts (contrairement aux nombres de , par exemple).
Nous verrons en particulier comment ils sont utilisés en cryptographie.
L’ensemble
Nous avons vu l’ensemble des entiers relatifs (positifs, négatifs ou nuls).
Pour , l’ensemble est défini comme l’ensemble des multiples de (la notation signifie littéralement « fois n’importe quel nombre de »).
Ainsi, est l’ensemble des nombres pairs, des nombres divisibles par (e.g. ), etc.
L’ensemble est un ensemble d’ensembles, dont les éléments sont les classes d’équivalence modulo .
Une classe d’équivalence modulo , c’est un ensemble de nombres de qui ont tous le même reste quand on considère leur division euclidienne par . En particulier, tous les nombres qui sont dans la même classe d’équivalence diffèrent d’un multiple de .
Par exemple :
- correspond à deux sous-ensembles, les nombres pairs et les nombres impairs
- correspond à trois sous-ensembles, qui sont les nombres de la forme , ceux de la forme et ceux de la forme .
- correspond à regrouper les nombres d’heures comptés à partir d’un temps , en fonction de ce qu’il donneraient, si on les affichait sur une horloge à cadran (et en ignorant les changements d’heure…)
- etc.
contient éléments, qui correspondent aux ensembles de nombres dont les restes modulo sont respectivement .
Par abus de langage, on notera les éléments de . Ils correspondent aux ensembles , , …, .
Addition sur
L’addition est compatible avec le calcul modulo .
Par exemple, d’une addition modulo ne change pas si on remplace l’un des nombres par un autre qui lui est égal modulo :
modulo
Cette observation nous permet de définir une table d’addition sur :
| + | 0 | 1 | 2 |
|---|---|---|---|
| 0 | 0 | 1 | 2 |
| 1 | 1 | 2 | 0 |
| 2 | 2 | 0 | 1 |
On définit une addition sur , en considérant le résultat modulo n de l’addition sur .
💡 Un ensemble muni d’une opération notée avec certaines propriétés similaires à l’addition sur s’appelle un groupe.
Multiplication sur
De la même façon, l’égalité suivante où sont des entiers quelconques, nous montre que la multiplication de est compatible avec le calcul modulo :
Par exemple, dans on aura (conséquence de modulo ).
On obtient une multiplication sur , en considérant le résultat modulo n de la multiplication sur .
On obtient par exemple la table de multiplication suivante sur :
| × | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 |
| 2 | 0 | 2 | 4 | 1 | 3 |
| 3 | 0 | 3 | 1 | 4 | 2 |
| 4 | 0 | 4 | 3 | 2 | 1 |
💡 Un ensemble muni des opérations et , avec des propriétés similaires à l’addition et la multiplication sur s’appelle un anneau.
Question : déterminer la table d’addition et de multiplication sur , à quelles opérations booléennes correspondent-elles ?
Éléments inversibles de
Observons la table de multiplication de :
| × | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 |
| 2 | 0 | 2 | 4 | 0 | 2 | 4 |
| 3 | 0 | 3 | 0 | 3 | 0 | 3 |
| 4 | 0 | 4 | 2 | 0 | 4 | 2 |
| 5 | 0 | 5 | 4 | 3 | 2 | 1 |
On remarque que l’on a les égalités suivantes :
La première égalité nous donne envie de dire que, pour la multiplication, est inversible et son inverse est .
En d’autres termes, une équation d’inconnue de la forme se résout en .
La seconde égalité nous montre en revanche que et ne peuvent pas être inversibles, car ils sont « diviseurs de zéro ». Si était inversible on pourrait réécrire l’égalité en .
On vérifie sur la table de multiplication que les éléments inversibles de sont et .
Retour sur l’identité de Bézout
L’algorithme d’Euclide permet d’obtenir l’identité suivante (je vous renvoie à l’article d’introduction à l’arithmétique, je remplace ici volontairement par , ce qui ne change pas le résultat) :
Il existe deux nombres tels que :
Que signifie pour un entier , l’existence d’un inverse dans ?
Cela traduit l’égalité modulo , ce qui signifie encore qu’il existe un entier tel que : .
En particulier, si , on peut construire des entiers et qui satisfont exactement cette égalité.
L’identité de Bézout nous indique donc que est inversible modulo si et seulement si et sont premiers entre eux.
C’est d’ailleurs bien ce que l’on constatait sur le cas au-dessus.
Question : Montrer que si l’on considère un nombre premier, tous les éléments non nuls de sont inversibles (pour la multiplication).
Fonction indicatrice d’Euler
On définit la fonction pour un entier appelée fonction indicatrice d’Euler, qui donne le nombre d’éléments inversibles pour la multiplication dans .
D’après ce qui précède, il s’agit du compte de nombres qui sont premiers avec .
💻 On peut calculer les premières valeurs de avec le script Python ci-dessous :
from math import gcdfor n in range(1, 100):print("phi({n}) = {phi}".format(n=n,phi=sum(1 for k in range(1, n + 1) if gcd(k, n) == 1)))phi(1) = 1phi(2) = 1phi(3) = 2phi(4) = 2phi(5) = 4phi(6) = 2phi(7) = 6...phi(95) = 72phi(96) = 32phi(97) = 96phi(98) = 42phi(99) = 60
Calcul de
Dans certains cas, on peut calculer simplement la fonction indicatrice d’Euler.
Par exemple, si est un nombre premier, alors car tous les nombres inférieurs à sont premiers avec .
Dans le cas où et sont des nombres premiers distincts, les nombres qui sont premiers avec sont ceux qui ne sont multiples ni de ni de .
- Les multiples de inférieurs à étant les nombres , il y en a .
- De même, il y a multiples de .
- Le seul multiple commun parmi ceux-ci est , qu’il ne faut donc compter qu’une fois.
On en déduit donc .
Théorème d’Euler
Le théorème d’Euler, qui date de 1761, peut se formuler ainsi :
Si est un entier premier avec , alors modulo .
On vérifiera par exemple que modulo .
On en déduit également, comme est premier, que modulo .
Ce dernier résultat montre à quel point le théorème d’Euler peut simplifier certains calculs ( est un nombre plus grand que le nombre d’atomes d’hydrogène dans le soleil…).
Une autre façon équivalente de formuler ce théorème, dans le langage de , est la suivante :
Si est inversible alors .
Nous allons donner l’idée de la preuve dans le cas de , dont voici la table de multiplication :
| × | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 0 | 2 | 4 | 6 | 1 | 3 | 5 |
| 3 | 0 | 3 | 6 | 2 | 5 | 1 | 4 |
| 4 | 0 | 4 | 1 | 5 | 2 | 6 | 3 |
| 5 | 0 | 5 | 3 | 1 | 6 | 4 | 2 |
| 6 | 0 | 6 | 5 | 4 | 3 | 2 | 1 |
Les éléments inversibles, au nombre de , sont (tous premiers avec , puisque est premier).
Considérons le produit de ces éléments .
En multipliant par on obtient :
On remarque en particulier que :
- le produit étant par définition constitué de éléments, on peut « répartir » les facteurs devant chaque élément du produit
- chaque nouveau facteur obtenu est un autre nombre, toujours inversible (car produit de deux nombres inversibles)
- les nombres inversibles obtenus sont deux-à-deux distincts, on a donc uniquement changé l’ordre des facteurs de
En simplifiant par (lui-même inversible), on obtient bien que = .
Question : En utilisant le théorème d’Euler et le calcul de où est un nombre premier, montrer le petit théorème de Fermat ci-dessous (historiquement, ce résultat fut découvert précédemment) :
Pour premier et un entier quelconque, on a modulo .
Application à la cryptographie
Nous avons vu précédemment comment le théorème d’Euler pouvait permettre de simplifier considérablement certains calculs comme modulo .
Ce résultat est au coeur d’un algorithme appelé RSA, qui permet de générer des clefs cryptographiques (clef privée et clef publique, on parle de cryptographie asymétrique) et de les utiliser pour chiffrer et déchiffrer des messages.
Voici comment fonctionnent les différentes parties de cet algorithme.
Génération des clefs
Choisir deux nombres premiers et et noter .
On a alors (voir le calcul de plus haut).Choisir un nombre premier avec .
Calculer un inverse de modulo : , où
Les clefs générées sont alors :
- Une clef publique :
- Une clef privée :
Nous discuterons plus loin de l’implémentation pratique des différentes étapes.
Chiffrement d’un message
Pour être chiffré, un message doit être encodé sous la forme d’un nombre .
Le message chiffré est obtenu par le calcul modulo suivant :
Une autre façon (équivalente) de formuler les choses est d’identifier un message en clair à un élément et calculer le message chiffré comme l’élément .
Déchiffrement d’un message chiffré
À partir du message chiffré , par construction un nombre entre et (inclus), on obtient le message déchiffré par la formule suivante :
Preuve du fonctionnement
Il s’agit de vérifier que la formule de déchiffrement de redonne bien le message d’origine.
On a par construction .
On développe alors la formule de déchiffrement :
On obtient deux cas. Le premier permet de conclure rapidement. Le second nécessite des calculs un peu plus compliqués…
- Si , le théorème d’Euler indique que et le calcul donne : on retrouve bien .
- Sinon, c’est que ou divise . Les deux ne peuvent être diviseurs simultanément puisque ), on peut supposer par exemple que divise .
On peut alors écrire , où et n’est divisible ni par ni par et est donc premier avec .
On obtient :
(on a utilisé que est premier avec , ce qui ramène au cas 1)
On a par ailleurs :
et aussi :
La dernière simplification vient du petit théorème de Fermat qui permet d’écrire , lorsque est premier et n’est pas divisible par .
Ces deux derniers calculs nous montrent que est divisible par et par , donc également par , ce qui nous permet de reprendre le calcul initial :
🙂
💻 Implémentation de RSA en Python
Nous avons décrit la recette de l’algorithme RSA, je vous en propose maintenant une implémentation basique en Python, afin de vérifier que tout cela fonctionne bien !
⚠️ Cette implémentation naïve ne doit évidemment pas être utilisée en production, elle n’est ni optimale ni robuste du point de vue de la sécurité. Son but est purement didactique.
Pour démarrer, cliquez sur le bouton Run ▶️, puis commencez par générer une paire de clefs.
Voici par exemple ce que j’ai obtenu :
Création des clefs
DEBUG: p=257205938468792623586345060713, q=564292122274801049105971923463,n=145139284880236882068996179284591347066612215282786124209119,e=5, d=29027856976047376413799235856753969801173724322018761444989Clef privée :eyJtb2R...3MzcyNDMyMjAxODc2MTQ0NDk4OX0=Clef publique :eyJtb2R..CAiZXhwb25lbnQiOiA1fQ==
Chiffrement
Entrez la clef publique :eyJtb2R..CAiZXhwb25lbnQiOiA1fQ==Message à chiffrer :Lorem ipsumMessage chiffré :12906681535323653913467296579360861757391479192915128204736
Déchiffrement
Entrez la clef privée :eyJtb2R...3MzcyNDMyMjAxODc2MTQ0NDk4OX0=Message à déchiffrer :12906681535323653913467296579360861757391479192915128204736Message déchiffré :Lorem ipsum
Quelques remarques
- Les clefs — couples (module, exposant) — sont sérialisées en utilisant
base64.
De façon générale, différentes implémentations de RSA peuvent utiliser différents formats pour représenter les clefs (nous y reviendrons). - L’étape 2 de l’algorithme de génération des clefs demande de générer premier avec .
Nous avons ici utilisé une méthode essai-erreur pour trouver une valeur de satisfaisante :e = 2while gcd(e, phi) != 1:e += 1
- Dans cette implémentation naïve, nous avons simplement codé en dur une liste de nombres premiers.
Le problème de la génération de grands nombres premiers est compliqué.
Beaucoup d’algorithmes reposent sur des méthodes probabilistes (le nombre généré pourrait ne pas être premier, mais la probabilité que ce soit le cas est négligeable, par exemple inférieure à ). - Le calcul de l’inverse modulaire est disponible nativement
dans Python à partir de la version 3.8 :
Si vous utilisez une version antérieure, vous pouvez utiliser l’implémentation de SymPy ou implémenter votre propre version (par exemple avec l’algorithme d’Euclide étendu, détaillé ici).d = pow(e, -1, phi)
RSA dans la vraie vie
Navigation en HTTPS
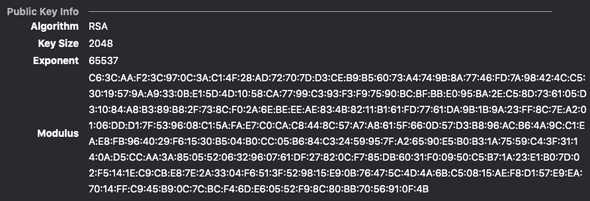
J’ai obtenu les informations ci-dessous avec Firefox en cliquant sur le petit symbole 🔒 à gauche de la barre d’adresse, depuis https://www.github.com.
On peut y lire notamment que :
- le certificat utilise RSA avec une clef sur 2048 bits : il s’agit de la taille du module généré.
- l’exposant est . Pour certaines raisons, ce nombre est très souvent utilisé comme exposant public.
- le contenu du module est également affiché (en hexadécimal)
Utilisation dans le cadre de TLS
En pratique, RSA est un algorithme assez lourd en terme de calculs et qui ne permet, comme nous l’avons vu, que de chiffrer des messages .
Dans le cadre de HTTPS et du protocole sous-jacent TLS, RSA peut être utilisé pour :
- authentifier le serveur à l’aide de sa clef publique (comme celle ci-dessus)
- échanger une clef de session, qui servira par exemple à l’établissement d’un chiffrement symétrique à l’aide d’un algorithme comme AES
D’autres algorithmes basés notamment sur les courbes elliptiques, objets mathématiques plus sophistiqués, constituent une alternative de plus en plus fréquente à RSA, en particulier pour l’échange de clef.
Décorticage de clefs avec OpenSSL
OpenSSL est une bibliothèque libre et ouverte de fonctionnalités cryptographiques, écrite en C. Elle est de fait très utilisée, par exemple par des serveurs web ou par OpenSSH.
Nous allons l’utiliser ici pour générer des vraies clefs, telles qu’elles sont utilisées en pratique.
La commande ci-dessous permet de générer une paire de clefs RSA 2048 bits, et de l’enregistrer
dans un fichier dummy.pem.
(Cette clef n’est évidemment pas utilisée en production. Le contenu est tronqué pour alléger la présentation.)
$ openssl genrsa -out dummy.pem 2048-----BEGIN RSA PRIVATE KEY-----MIIEowIBAAKCAQEAxZTA6Tlfs+/le2obemsioULR3ipwupIXvnATYGpjpbdLsKEnHJnoOl/IoeQHzDcS10/NKHWWklcK4WfxnRX62XyyWYmnnfJQPLepGPujbPYsxLAul4ON9INOulHXHKrorqyQNvzeCm46gQAeEd2+IH2HtFHEM2Avtw0qYxQc5y0rEeTQ...v+gagQKBgFHsYq9M8E7Po67DNfK9f0qfxev1PTV584vVWs4O0vr2p/+RorEed3XaW02mZnqg0wS/4wuKz43UUU9x8GEZuNIW0/5XX/YrvEV90OktQ9lbanNLWJaqSyoC6PLdT49uniyhkiySmVt9EgJSIaYy32F3HCYaNWkF9pyZ+SNXlB23-----END RSA PRIVATE KEY-----
La commande suivante permet d’examiner un tel fichier pour voir ce qu’il contient :
$ openssl rsa -text -noout < dummy.pemPrivate-Key: (2048 bit)modulus:00:c5:94:c0:e9:39:5f:b3:ef:e5:7b:6a:1b:7a:6b:22:a1:42:d1:de:2a:70:ba:92:17:be:70:13:60:6a:...08:32:9a:2c:57:cc:3c:1b:08:1f:1f:e4:38:de:a4:40:43:98:39:56:70:d5:d5:03:71:1f:3a:06:dd:d0:da:6fpublicExponent: 65537 (0x10001)privateExponent:4d:9d:b6:fe:a7:84:39:fa:66:8a:c9:cf:0b:93:24:...38:1c:d4:5c:1e:67:37:08:6a:81:cf:56:ad:8f:b5:11prime1:00:fe:94:9b:60:59:99:11:4c:8d:48:f4:a4:39:af:...b9:f0:d6:3b:d9:f4:4d:d3:07prime2:00:c6:ae:c8:d8:32:17:25:bc:89:86:cc:b2:38:e7:...6f:ba:ac:12:be:7a:89:5b:59exponent1:00:ae:b5:ed:ab:c1:d1:7a:3d:be:f8:42:6c:31:ea:...7c:dc:fb:29:37:fa:a1:2e:21exponent2:0a:d1:19:3e:2b:fb:f6:a1:fd:1a:c9:aa:2a:4e:f6:...3f:61:7e:e3:bf:e8:1a:81coefficient:51:ec:62:af:4c:f0:4e:cf:a3:ae:c3:35:f2:bd:7f:...9c:99:f9:23:57:94:1d:b7
Nous pouvons faire les observations suivantes :
- Ce format encode les deux clefs (privées et publique) dans le même fichier.
La commande
openssl rsa -in dummy.pem -puboutpermet d’en extraire une clef publique. - Le fichier stocke le module et les exposants (public) et (privée), mais aussi d’autres données.
Ces informations supplémentaires permettent d’optimiser la fonction de déchiffrement du message, le calcul pouvant alors être rendu plus rapide.
Cette optimisation, appelée RSA-CRT, utilise le théorème des restes chinois.
Attaques contre RSA
RSA reste très largement utilisé, mais des scénarios d’attaque sont connus si les clefs ne respectent pas certaines contraintes.
En particulier, le module doit être suffisamment grand pour rendre extrêmement complexe sa factorisation (aujourd’hui, on considère qu’il faut une taille de clef d’au moins bits).
D’autres scénarios d’attaque existent, par exemple l’attaque de Wiener, qui permet de retrouver la clef privée à partir de la clef publique lorsque est trop petit.
Un exercice intéressant pourrait être de la mettre en oeuvre pour casser l’implémentation naïve fournie plus haut…
Maths et applications, avec les mains et avec du code 💻
Suivre sur Twitter