La géométrie projective, d'Urbino à OpenGL

30 juillet 2021

J’ai pris la photographie ci-dessous en marchant sur une voie désaffectée (la petite ceinture).

Face à cette scène, je peux montrer du doigt un point où les deux rails semblent s’intersecter.

Ce point n’existe pas physiquement mais il semble bien réel dans l’image que nous percevons.

Les peintres de la Renaissance italienne parleraient de point de fuite.

Le formalisme mathématique de la géométrie projective, que nous abordons ici, permet également de lui donner une existence : à chaque point du sol correspond une direction pointée par l’observateur.

Le « point » d’intersection des rails, lui, correspond à une direction parallèle au plan du sol.

Le plan projectif réel

Dans l’image ci-dessus, nous pouvons distinguer les éléments suivants :

• Un observateur $O$, dont nous prendrons la position comme origine d’un repère cartésien de l’espace.
• Le plan du sol, que nous assimilerons au plan $z = 1$ (ce choix simplifie certaines expressions, il demande ici de considérer l’image à l’envers)
• Les deux rails, qui correspondent à des droites parallèles, dans le plan du sol ($z = 1$).

On appelle plan projectif l’ensemble des droites de l’espace qui passent par $O$.

Identification avec les points du plan $z = 1$

Chaque point $P \neq O$ de l’espace définit une droite $(OP)$.

Réciproquement, si l’on se donne une droite $D$ passant par l’origine, on a un (et un seul) des cas suivants :

• il existe un point $P$ du plan $z = 1$ tel que $D = (OP)$, un tel point $P$ est alors unique
• $D$ est parallèle au plan $z = 1$ (vis-à-vis de ce plan, $D$ jouera le rôle d’un point à l’infini)

Cette identification formalise l’idée suivante :

Si l’on particularise un plan ne passant pas par l’origine, on a informellement : Plan projectif = Points de ce plan + Points à l’infini

Nous parlerons d’ailleurs de points pour désigner les éléments du plan projectif.

Coordonnées homogènes

Si $P = (x, y, z) \neq O$ est un point de l’espace, on désigne par $[x:y:z]$ le point du plan projectif correspondant.

Les points $(\lambda x, \lambda y, \lambda z)$ de l’espace, pour $\lambda \neq 0$, se trouvent tous sur la même droite passant par $O$.

Les notations $[\lambda x:\lambda y:\lambda z]$ et $[x:y:z]$ désignent donc le même point (du plan projectif).

Ces sont des coordonnées homogènes de ce point. 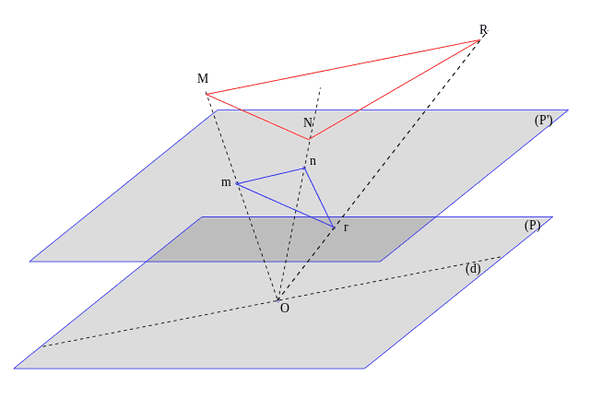Sur l’image ci-dessus, les coordonnées dans l’espace des points $m$ et $M$ donnent deux triplets de coordonnées homogènes désignant le même point du plan projectif, associé à la droite $(OM)$.

Convergence dans le plan projectif

Considérons la suite de points de coordonnées (homogènes) $[1:n:1]$.

Ces points sont aussi représentés par les coordonnées $[{1 \over n}:1:{1 \over n}]$.

Cette suite converge vers un point de coordonnées ${[0:1:0]}$, associé à une droite du plan $z = 0$ : c’est un point à l’infini vis-à-vis du plan $z = 1$.

Si l’on considère la suite de points de coordonnées $[-1:n:1]$, elle converge aussi vers ce même point : on retrouve la notion de convergence des deux rails parallèles vers un point à l’infini, en dehors du plan $z = 1$.

Cette notion de point à l’infini est toutefois relative : vis-à-vis du plan $y = 1$, le point ${[0:1:0]}$ est un point « classique ».

Perspective et vision en 3D

Le fait que les lignes parallèles dans le champ de vision d’un observateur semblent « converger » vers un point fictif (le point de fuite) est l’une des découvertes de la Renaissance italienne.

La position de ce point conditionne le degré de convergence des lignes associées, qui fait partie des indicateurs visuels permettant à notre cerveau d’apprécier les distances.

(D’autres facteurs existent, ils sont par exemple évoqués dans le chapitre 5 du livre The Eye: A Very Short Introduction)

Ci-dessous, La Cité idéale, peinture du XV^ème siècle conservée à Urbino, qui utilise un point de fuite central pour recréer l’impression de profondeur.

De multiples points à l’infini

Par rapport à un plan $z = 1$, les points à l’infini correspondent aux droites parallèles à ce plan qui passent par l’origine. En terme de coordonnées homogènes, elles correspondent à des points de coordonnées $[x, y, 0]$, pour $(x, y) \neq (0, 0)$.

Il y en a donc autant que de directions dans le plan.

En considérant un sous-ensemble régulier du plan, comme les points de coordonnées entières, on obtient un réseau.

Dans ce cas, les points à l’infini correspondent à des directions données par des droites de pentes rationnelles.

Cette photographie d’un champ de lavande, publiée par François Rouvière sur son site, permet de distinguer certains points à l’infini — combien en comptez-vous ?

L’espace projectif $P^3(\R)$ et OpenGL

Le plan projectif permet d’introduire des points à l’infini par rapport à un plan, en considérant les droites de l’espace à trois dimensions.

Cette construction se généralise, pour donner la notion d’espace projectif réel de dimension $n$ :

L’espace projectif réel de dimension $n$, noté $P^n(\R)$, est l’ensemble des droites vectorielles de $\R^{n+1}$.

💡 De façon plus rigoureuse, on définit les espaces projectifs sous la forme d’ensembles quotients. Ils héritent notamment de la topologie quotient permettant de formaliser la notion de convergence.

Exemples :

• $P^2(\R)$ est le plan projectif réel que nous avons présenté précédemment.
• $P^1(\R)$ est la droite projective réelle, que l’on obtient en ajoutant aux réels un unique point à l’infini $\infty$. Cette droite est topologiquement équivalente à un cercle.

L’espace projectif $P^3(\R)$

L’espace projectif $P^3(\R)$ (que nous désignerons simplement par espace projectif), se construit de façon très similaire au plan projectif, en considérant les droites passant par l’origine dans l’espace à quatre dimensions $\R^4$.

Un point de $\R^4$ différent de l’origine étant repéré par ses coordoonées ${(x, y, z, w)}$, on peut également utiliser des coordonnées homogènes pour désigner les points de l’espace projectif :

$[x, y, z, w]$ désigne alors la droite vectorielle colinéaire au vecteur $(x, y, z, w)$.

Dès lors, on peut particulariser le sous-espace (à trois dimensions) $w = 1$ et considérer les deux cas possibles :

• Cas $w \neq 0$ : $[x, y, z, w]$ désigne le même point que $[{x \over w}, {y \over w}, {z \over w}, 1]$, qui correspond à un unique point $({x \over w}, {y \over w}, {z \over w})$ du sous-espace $w = 1$.
• Cas $w = 0$ : on peut identifier $[x, y, z, 0]$ à un point à l’infini vis-à-vis de l’espace $w = 1$. Il correspond à la direction des droites parallèles au vecteur $(x, y, z)$ dans cet espace.

💻 Ordinateurs et 3D

OpenGL définit un ensemble de standard (API) permettant d’interagir avec une carte graphique, dans le but notamment de représenter des scènes en trois dimensions sur un écran d’ordinateur.

Un exemple d’objet que l’on souhaite pouvoir modéliser dans une scène 3D est une source de lumière.

En représentant la position d’une source de lumière par des coordonnées homogènes $[x, y, z, w]$, on peut gérer les deux cas classiques :

• Source ponctuelle ($w = 1$), qui correspond à une source de lumière dans la scène ou à distance finie — par exemple une ampoule ou une bougie.
• Source directionnelle ($w = 0$), qui correspond au cas d’une source de lumière à l’infini, comme le soleil. Les coordonnées permettent alors de préciser sa direction.

L’utilisation de matrices $4 \times 4$ permet de représenter d’une façon unifiée différentes transformations: translations, rotations, facteur d’échelle, etc.

Par exemple, je vous laisse vérifier que l’opération ci-dessus correspond à une translation de $u$ selon l’axe des $x$ :

On remarquera en particulier que pour un point à l’infini ($w = 0$), cette opération n’a pas d’effet.

Lorsque l’on se déplace dans le décor, la position (relative) d’une bougie change, mais la direction du soleil est inchangée.

Espaces projectifs sur un corps quelconque

Les espaces projectifs peuvent être axiomatisés d’une façon purement algébrique.

Les constructions précédentes peuvent alors se généraliser sur tout ensemble muni d’une structure de corps.

En remplaçant les réels par les nombres complexes on construit ainsi les espaces projectifs $P^n(\Complex)$.

Par exemple, $P^1(\Complex)$ est la droite projective complexe, qui correspond à l’ajout d’un point à l’infini au plan complexe (de coordonnées homogènes $[z, 0]$ où $z \neq 0$ est un nombre complexe). Topologiquement, cet espace revient à refermer le plan complexe pour obtenir une sphère, la sphère de Riemann.

Géométrie projective en caractéristique $p > 0$

Sur les corps de caractéristique non-nulle $p$ (où $\underbrace{1 + 1 + ... + 1}_{\text{p fois}} = 0$), on peut aussi définir des espaces projectifs.

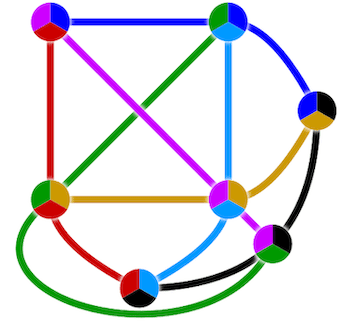
Par exemple, dans le cas du corps fini à deux éléments $F_2$, le plan projectif $P^2(F_2)$ (plan de Fano) peut se représenter ainsi :

Le carré correspond aux quatre points de coordonnées $(0, 0, 1)$, $(0, 1, 1)$, $(1, 0, 1)$ et $(1, 1, 1)$. Il est complété par trois points à l’infini $(0, 1, 0)$, $(1, 0, 0)$ et $(1, 1, 0)$.

En connectant par une ligne d’une même couleur les points d’une même droite (y compris le point à l’infini correspondant), on vérifie les propriétés d’incidence :

• Par deux points distincts passent une et une seule droite
• Deux droites distinctes se coupent en un et un seul point

💡 Remarquons que l’on obtient le plan $(F_2)^2$ par réduction des coordonnées du réseau $\Z^2$ modulo $2$.

Dans le cas d’une réduction modulo $4$ (non premier), une égalité comme ${2 \times (2, 2) = (0, 0)}$ montre que les concepts développés pour le plan projectif réel ne se transfèrent pas tels quels…

On pourra néanmoins construire des espaces projectifs sur les corps finis non-premiers (de cardinal $p^n$ pour $p$ premier et $n > 1$), l’interprétation géométrique étant moins aisée.

Homogénéisation des équations algébriques

Nous avons parlé de droites dans le plan projectif, sans vraiment définir de quoi il s’agit.

Dans un plan classique (Euclidien), une droite est définie par une équation de la forme $a x + b y + c = 0$, où $(a, b) \neq (0, 0)$.

Dans le plan projectif, cette équation devient une équation sur les coordonnées homogènes de la forme $a x + b y + c z = 0$ :

• on retrouve la droite (du plan Euclidien) en particularisant le plan $z = 1$
• l’unique point (projectif) vérifiant $z = 0$ est le point à l’infini, dont des coordonnées homogènes sont $[b:-a:0]$.

Je vous laisse vérifier qu’avec cette définition, deux droites (projectives) se coupent toujours en un unique point (projectif).

💡 Vers la géométrie algébrique…

De façon générale, une équation polynômiale à $n$ variables sur un corps $K$ s’homogénéise pour donner une équation dans l’espace projectif $P^n(K)$.

L’équation ${x^2 - y^2 - 1 = 0}$ correspond ainsi à l’équation homogène ${x^2 - y^2 - z^2 = 0}$ : on retrouve une caractérisation des coniques.

Dans le cas du plan projectif sur un corps algébriquement clos (par exemple $\Complex$, ou la clôture algébrique $\bar{F_p}$ d’un corps fini), le résultat obtenu sur l’intersection de deux droites se généralise.

Le théorème de Bézout indique que deux polynômes (dans $K[X, Y]$) de degrés respectifs $d_1$ et $d_2$ et sans facteur commun, définissent deux courbes qui ont ${d_1 \cdot d_2}$ points d’intersection dans le plan projectif (comptés avec leurs multiplicités).

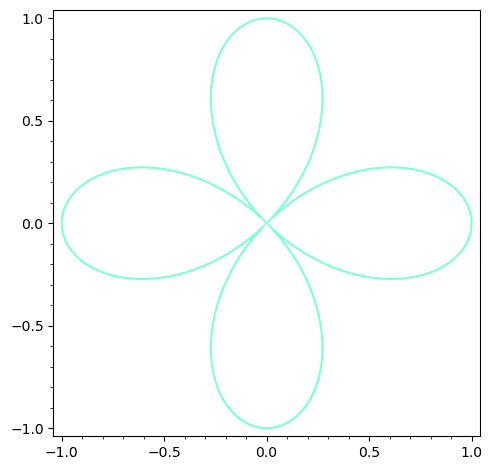
Quadrifolium

Ci-dessous, une courbe algébrique de degré $6$, d’équation ${(x^2 + y^2)^3 - (x^2 - y^2)^2 = 0}$ :

Questions :

• Déterminer sur cette figure une droite intersectant la courbe en $6$ points.
• Montrer que cette courbe n’a aucun point à l’infini.
• Justifier que l’intersection de cette courbe avec une ellipse ne peut comporter plus de $12$ points. Déterminer une ellipse qui réalise l’égalité (solution).
• En considérant les solutions dans $\Complex^3$ de l’équation homogène associée au quadrifolium, déterminer ses points à l’infini dans $P^2(\Complex)$.

L’étude des courbes algébriques fait partie d’un vaste domaine des mathématiques, la géométrie algébrique.

Pour une introduction à ce sujet (pas facile…), on pourra lire par exemple Algebraic Curves: An Introduction to Algebraic Geometry de William Fulton.

💻 Cryptographie sur les courbes elliptiques

Nous avons déjà évoqué, dans un article précédent, l’utilisation de courbes elliptiques en cryptographie.

Curve25519 est un exemple de courbe elliptique définie sur le corps $F_p$ à $p = 2^{255} - 19$ éléments par l’équation ${y^2 = x^3 + 486662 x^2 + x}$.

Question : Déterminer le point à l’infini de cette courbe dans $P^2(F_p)$.

Ce point à l’infini sera encodé de différentes façons suivant la courbe et le système de coordonnées utilisés dans les implémentations de cryptographie sur courbes elliptiques (OpenSSL, go/crypto, etc.).

Maths et applications, avec les mains et avec du code 💻
Suivre sur Twitter

• ← Nombres premiers, Miller-Rabin et OpenSSL
• Transformée de Fourier discrète et multiplications →