Quelques aspects de la mécanisation de la géométrie

07 juillet 2024 — Géométrie, Logique, Intelligence Artificielle

En début d’année 2024, des chercheurs de DeepMind annoncent AlphaGeometry : un logiciel capable de résoudre des problèmes de géométrie posés aux Olympiades Internationales de Mathématiques, avec un niveau comparable aux meilleurs participants.

On pourrait arguer qu’il s’agit de la continuité d’un processus dont Euclide fut, il y a plus de deux millénaires, l’un des précurseurs : la mécanisation du raisonnement géométrique.

Les Éléments d’Euclide exposent une théorie de la géométrie plane fondée sur cinq postulats dont sont déduites plus d’une centaine de propositions. La géométrie qui y est présentée fait exclusivement référence aux figures et à leurs propriétés, sans utilisation de la notion de nombre — on parle parfois de géométrie synthétique, par opposition à la géométrie analytique.

Au regard des standards des mathématiques actuelles, les Éléments d’Euclide sont néanmoins considérés comme insatisfaisants sur le plan de la rigueur.

J’aimerais, dans cet article, évoquer ce sujet ainsi que d’autres développements plus récents, qui illustrent la façon dont le raisonnement géométrique a été mécanisé, jusqu’à pouvoir être automatisé dans des programmes informatiques.

Lacunes des Éléments : l’exemple de l’axiome de Pasch

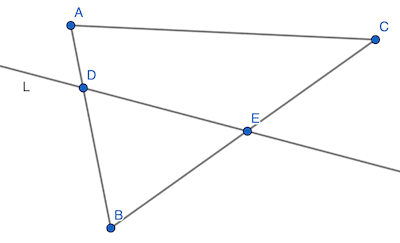
Soient $A, B, C$ trois points non alignés et $L$ une droite du plan $ABC$ qui ne passe par aucun des points $A, B, C$ ; si la droite $L$ passe par l’un des points du segment $AB$, elle passe ou par un point du segment $BC$ ou par un point du segment $AC$.

Cet énoncé, qui est une évidence lorsque l’on considère une représentation graphique comme celle ci-dessus, est connu sous le nom d’axiome de Pasch. Il est utilisé à plusieurs reprises dans des démonstrations des Éléments bien qu’il ne fasse pas partie des axiomes d’Euclide et ne soit jamais démontré.

De fait, une telle démonstration serait impossible : on peut construire (mais ce n’est pas simple) des géométries dans lesquelles l’axiome de Pasch est mis en défaut bien que les cinq axiomes d’Euclide y soient vérifiés.

Le fait qu’Euclide utilise implicitement des « évidences » que ses axiomes ne permettent pas de prouver a conduit, à partir du 19ème siècle, à considérer cette théorie comme insatisfaisante sur le plan de la rigueur.

C’est dans ce contexte que Hilbert puis Tarski proposeront de nouvelles axiomatisations de la géométrie du plan.

Hilbert et la notion d’ordre le long d’une droite

Dans ses Fondements de la Géométrie (1899), Hilbert pose une vingtaine de postulats qui formalisent notamment la notion d’ordre le long d’une droite : on note $A \star B \star C$ si $A$, $B$ et $C$ sont alignés, et $B$ se trouve entre $A$ et $C$.

Cette notion lui permet d’introduire, entre autres, l’axiome de Pasch sous la forme suivante :

Axiome de Pasch (Hilbert)

Si $A$, $B$, $C$ sont trois points non alignés, $L$ une droite ne contenant aucun de ces trois points et contenant un point $D$ vérifiant $A \star D \star B$, alors $L$ contient un point $E$ vérifiant $A \star E \star C$ ou (exclusif) $L$ contient un point $E$ vérifiant $B \star E \star C$.

Tarski et la logique du premier ordre

Dans le contexte de la recherche de fondements rigoureux pour établir leurs résultats, les mathématiciens élaborent au début du 20ème siècle un langage et un cadre formel permettant de présenter des théories.

Ce cadre formel prendra le nom de logique du premier ordre et servira notamment à formuler la théorie des ensembles ou l’arithmétique. On peut considérer qu’il s’agit aujourd’hui d’une façon standard de présenter une théorie mathématique.

En 1926, Tarski présente une théorie de la géométrie plane formulée intégralement en logique du premier ordre. Son formalisme repose sur les concepts de congruence (noté $\equiv$) et d’ordre le long d’une droite (utilisant ici le symbole $B$, pour betweenness) et ses axiomes sont donnés de façon purement symbolique, par exemple :

Axiome de Pasch (Tarski)

$(B{adc} \land B{ubc}) \implies \exists e (B{deu} \land B{bea})$

Exercice :

• Dessiner une figure correspondant à la formule ci-dessus — en particulier, on remarquera l’introduction d’un point $u$ par rapport à la version de l’axiome utilisée par Hilbert — et interpréter ce résultat.
• Se convaincre que cette version de l’axiome de Pasch, contrairement à celle de Hilbert, reste valable dans l’espace à trois dimensions.

Un des intérêts de l’utilisation de la logique du premier ordre est que celle-ci permet de faire porter le raisonnement logique par la syntaxe — via des manipulations de formules comme celle ci-dessus. Les « évidences », issues de notre intuition ou de représentations graphiques, doivent alors être formalisées dans le langage et pouvoir être démontrées mécaniquement à partir des axiomes.

Preuves formelles informatisées : l’exemple de GeoCoq

Au cours du 20ème siècle, le développement de l’informatique, tant sur le plan théorique que matériel, amène progressivement la question de l’automatisation de la vérification de preuve. Le cadre théorique moderne, dans lequel les questions d’axiomatisation et de démonstration se traduisent en termes de manipulations mécaniques de formules, s’y prête particulièrement bien.

De nos jours, de nombreux assistants de preuve sont disponibles et couvrent une bonne partie des domaines mathématiques.

Coq, créé en 1984 à l’INRIA, est l’un d’entre eux. Concrètement, cet assistant définit un langage de programmation dans lequel on peut formuler des énoncés et preuves mathématiques, et un moteur capable de vérifier la validité d’une telle preuve.

Pour certaines raisons, que j’ai déjà évoquées dans un article précédent, Coq utilise abondamment le système de typage de son langage de programmation, les propositions y étant incarnées par des types.

GeoCoq est un projet développé en Coq, qui vise à formaliser les fondements de la géométrie Euclidienne dans ce langage et intègre en particulier une implémentation des axiomes de Hilbert et des axiomes de Tarski.

💡 L’axiomatisation de Hilbert implémentée dans GeoCoq ne reprend pas les deux axiomes de continuité de la présentation originale de Hilbert. En effet, ces axiomes ne sont pas rigoureux au sens de la logique moderne. Par exemple, l’axiome d’Archimède fait référence au concept d’entier naturel, sans que les propriétés de ceux-ci ne soient formalisées dans sa théorie. On pourra lire le livre Geometry: Euclid and Beyond de Robin Hartshorne pour une présentation approfondie des axiomes et de la géométrie de Hilbert.

À titre d’exemples, voici les types implémentant l’axiome de Pasch de chacune de ces théories :

Axiome de Pasch, formalisme de Hilbert (source)

pasch :
  ∀ A B C l,
    ¬ ColH A B C → ¬ Incid C l → cut l A B →
    cut l A C ∨ cut l B C;

Axiome de Pasch, formalisme de Tarski (source)

inner_pasch : forall A B C P Q,
  Bet A P C -> Bet B Q C ->
  exists X, Bet P X B /\ Bet Q X A;

Grâce à ces axiomatisations, l’équipe de GeoCoq a pu prouver informatiquement des résultats d’équivalence entre différentes théories de la géométrie plane — on pourra lire par exemple le papier From Hilbert to Tarski à ce sujet.

Une question qui se pose naturellement à ce stade est de savoir si, et comment, les ordinateurs pourraient être utilisés pour générer automatiquement des démonstrations ?

Il existe à ce sujet des approches purement symboliques, que je ne développerai pas — je vous renvoie à l’article A Decision Procedure for Geometry in Coq qui en évoque quelques-unes.

AlphaGeometry et le raisonnement neuro-symbolique

L’approche des équipes de DeepMind pour élaborer AlphaGeometry s’inscrit dans un cadre différent, puisqu’il s’agit d’un système neuro-symbolique.

Je reviendrai un peu plus loin sur ce que cela signifie, regardons pour l’instant un exemple simple de problème résolu par ce logiciel.

Un exemple : l’orthocentre

L’énoncé suivant, qui se trouve dans la documentation d’AlphaGeometry, exprime le fait que les trois hauteurs d’un triangle ABC se coupent en un point $D$, l’orthocentre (on_tline d b a c signifie que $DB$ est orthogonal à $AC$) :

orthocenter
a b c = triangle a b c; d = on_tline d b a c, on_tline d c a b ? perp a d b c

L’existence de l’orthocentre est un résultat assez classique de géométrie dont il existe différentes preuves, voici celle que produit AlphaGeometry :

* From theorem premises:
A B C D : Points
BD ⟂ AC [00]
CD ⟂ AB [01]
 * Auxiliary Constructions:
E : Points
E,B,D are collinear [02]
E,C,A are collinear [03]
 * Proof steps:
1.   E,B,D are collinear [02] & E,C,A are collinear [03] & BD ⟂ AC [00]
     ⇒  ∠BEA = ∠CED [04]
2.   E,B,D are collinear [02] & E,C,A are collinear [03] & BD ⟂ AC [00]
     ⇒  ∠BEC = ∠AED [05]
3.   A,E,C are collinear [03] & E,B,D are collinear [02] & AC ⟂ BD [00]
     ⇒  EC ⟂ EB [06]
4.   EC ⟂ EB [06] & CD ⟂ AB [01] ⇒  ∠(EC-BA) = ∠(EB-CD) [07]
5.   E,C,A are collinear [03] & E,B,D are collinear [02] & ∠(EC-BA) = ∠(EB-CD) [07]
     ⇒  ∠BAE = ∠CDE [08]
6.   ∠BEA = ∠CED [04] & ∠BAE = ∠CDE [08] (Similar Triangles)⇒  EB:EC = EA:ED [09]
7.   EB:EC = EA:ED [09] & ∠BEC = ∠AED [05] (Similar Triangles)⇒  ∠BCE = ∠ADE [10]
8.   EB:EC = EA:ED [09] & ∠BEC = ∠AED [05] (Similar Triangles)⇒  ∠EBC = ∠EAD [11]
9.   ∠BCE = ∠ADE [10] & E,C,A are collinear [03] & E,B,D are collinear [02]
     & ∠EBC = ∠EAD [11] ⇒  AD ⟂ BC

Notons tout d’abord que la preuve conçue par AlphaGeometry est exprimée dans un langage formel qui reprend les notions classiques de géométrie synthétique (angles, colinéarité, similarité, etc.), mais qui ne correspond à aucun des formalismes historiques présentés précédemment (Hilbert, Tarski).

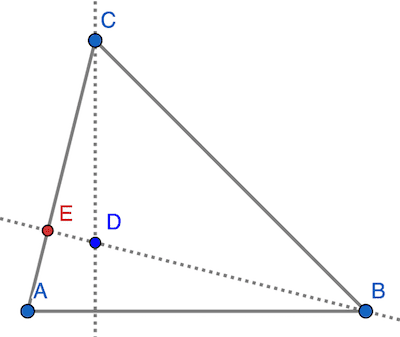
Concernant le processus de résolution, remarquons l’introduction d’un point intermédiaire $E$, qui ne fait pas partie des données initiales .

Le dessin ci-dessous illustre la situation du problème, je vous laisse vérifier les neuf étapes de la résolution, qui ne comportent pas de difficulté particulière.

Principes de fonctionnement

AlphaGeometry est basé sur une approche neuro-symbolique, c’est-à-dire qu’il combine les deux types d’éléments suivants :

• Un réseau de neurones — en l’occurrence, ce réseau implémente un modèle de langue (LLM). Dans le cas d’AlphaGeometry, les équipes de DeepMind ont utilisé un modèle maison, basé sur leur bibliothèque Meliad et comportant 152 millions de paramètres.
• Un système symbolique, basé sur un langage formel auquel correspond un logiciel de vérification de preuves. De fait, il semble qu’AlphaGeometry repose sur une variante du logiciel GEX — je n’ai malheureusement pas trouvé d’information concernant ce logiciel et les axiomes utilisés.

L’idée parfois avancée pour justifier une telle approche est qu’elle correspondrait aux deux systèmes de pensée du cerveau humain, tels que popularisés par Daniel Kahneman : intuitif et rapide pour le premier, lent et logique pour le second.

Dans le cas d’AlphaGeometry, le système symbolique lui-même est assez élaboré puisqu’il intègre un moteur de génération de preuve capable, étant donnée une construction géométrique, de dériver des résultats non triviaux associés à cette construction. Le modèle de langue est en fait utilisé exclusivement pour l’ajout de constructions intermédiaires (auxiliary constructions), comme le point $E$ de l’exemple précédent.

Entraînement du modèle

De façon très simpliste, un modèle de langue est un programme qui, étant donné un début de phrase, propose un mot suivant pour la compléter — ou, généralement, un ensemble de mots possibles avec une estimation de probabilité associée à chacun d’eux.

Un tel modèle est conçu par entraînement sur un corpus de texte : par utilisation de diverses heuristiques, les phrases sont transformées dans des représentations vectorielles portant une information sémantique et le système apprend statistiquement à générer un mot suivant qui respecte cette sémantique.

Un des problèmes que les concepteurs d’AlphaGeometry ont dû surmonter est que cette approche suppose l’existence d’un corpus de texte important. Lorsqu’il s’agit d’entraîner un programme à écrire du code dans un langage de programmation comme Python, des corpus écrits par des humains sont déjà disponibles (GitHub, etc.). Ce n’est pas le cas pour les langages formels, qui sont aujourd’hui confinés à un usage de niche.

L’approche retenue pour AlphaGeometry permet de s’affranchir de cette contrainte : le jeu de données d’entraînement a été entièrement généré par la machine — on parle de données synthétiques.

Plus précisément, le jeu de données consiste en une liste d’entrées, chacune de la forme $(\text{Prémisses}, \text{Théorème}, \text{Démonstration})$. Elles sont construites de la façon suivante :

1. Une construction géométrique est générée aléatoirement. Celle-ci pourra par exemple consister en un ensemble de points $A, B, C, D, E$ et un ensemble $R$ de relations géométriques entre ces points.
2. Un moteur de déduction purement symbolique va dériver, à partir de ces relations, des lemmes géométriques. On obtient ainsi par expansion un graphe direct acyclique de lemmes géométriques.
3. Un nœud $N$ de ce graphe, correspondant à un certain lemme, est retenu comme théorème. Si ce théorème concerne un sous-ensemble $S$ des points introduits initialement (par exemple $S = \{A, B, C, D\}$) mais dépend (via un nœud du graphe) d’un point qui n’est pas dans $S$ (par exemple $E$), ce point est considéré comme une construction intermédiaire.
4. Par extraction du sous-graphe $G(N)$, comportant le nœud $N$ et ses dépendances, on obtient une démonstration du théorème. Les points de $S$ et le sous-ensemble de $R$ des relations portant sur ces points en constituent les prémisses.

En procédant ainsi, l’équipe d’AlphaGeometry a pu générer 100 millions de triplets $(\text{Prémisses}, \text{Théorème}, \text{Démonstration})$ dont 9 millions comportent au moins une construction intermédiaire, données qu’ils ont utilisées pour entraîner leur modèle à générer des constructions intermédiaires.

Dans l’une des preuves générées par AlphaGeometry, concernant un problème posé aux olympiades de 2015, le modèle a ainsi introduit 3 points intermédiaires, au sein d’une preuve comportant en tout 112 étapes.

Pour plus d’information à ce sujet, et des exemples plus élaborés, je vous invite à lire l’article Solving olympiad geometry without human demonstrations publié dans Nature par les auteurs d’AlphaGeometry.

Maths et applications, avec les mains et avec du code 💻
Suivre sur Twitter

• ← Automates, expressions régulières et arithmétique de Presburger