Satisfaisabilité, frustration et transitions de phase
11 janvier 2025 — Rust, Informatique théorique, Physique
Vous êtes chargé des invitations pour une grande fête familiale, mais vos proches vous ont imposé certaines conditions :
- Votre mère vous demande d’inviter Pierre, ou de ne pas inviter Romane.
- Votre frère vous demande d’inviter Romane ou Quentin (ou les deux).
- Votre oncle, lui, veut snober soit Quentin soit Pierre (soit les deux).
Question : Existe-t-il une liste d’invités qui satisfasse toutes ces clauses ?
Les conditions énoncées dans le petit problème présenté ci-dessus peuvent se résumer dans la formule logique suivante :
Il se trouve que cette formule est satisfaisable, par exemple en invitant Pierre et Romane, mais en excluant Quentin.
Intuitivement, on peut imaginer que plus on ajoute de clauses à une formule, moins elle a de chances d’être satisfaisable.
Dans cet article, nous allons vérifier expérimentalement cette intuition et mettre en évidence un phénomène de transition de phase entre un régime de satisfaisabilité et un régime de non-satisfaisabilité des formules, lorsque le nombre de clauses augmente.
Nous verrons dans un second temps comment ce problème peut se traduire en termes énergétiques, par analogie avec certains modèles physiques.
Quelques mots sur la satisfaisabilité
Le problème de satisfaisabilité booléenne (SAT) s’intéresse à des formules constituées à l’aide des opérateurs logiques (ou), (et), (non).
Les propriétés de ces opérateurs logiques permettent de transformer toute formule ainsi formée en une formule équivalente sous forme normale conjonctive (CNF), comme celle présentée en introduction :
Cette formule est constituée d’une conjonction () de clauses, chacune de ces clauses étant constituée d’une disjonction () de littéraux (une variable ou sa négation).
Le problème de la satisfaisabilité consiste à se demander si l’on peut attribuer à chaque variable intervenant dans la formule une valeur de vérité de façon à ce que la formule soit vérifiée.
Dans ce cas c’est possible, par exemple avec les assignations suivantes :
| Variable | Valeur |
|---|---|
| Pierre | Vrai |
| Quentin | Faux |
| Romane | Vrai |
Algorithmes de résolution
Le problème de déterminer, pour une formule booléenne quelconque, si elle est satisfaisable, s’appelle le problème SAT.
Le problème k-SAT consiste à déterminer la satisfaisabilité d’une formule sous forme normale conjonctive dont les clauses sont toutes de taille . Par exemple, la formule présentée précédemment correspond à : ses clauses sont toutes composées de deux littéraux.
Les problèmes SAT et k-SAT () sont des problèmes NP-complet, mais on peut les résoudre en un temps raisonnable dans beaucoup de cas grâce à des algorithmes de backtracking.
💡 Le cas de 2-SAT
Le problème 2-SAT peut se résoudre en temps polynomial.
L’algorithme implémenté ici consiste, par exemple, à remarquer qu’une clause comme est équivalente aux implications et .
On construit alors un graphe orienté dont les sommets correspondent aux littéraux (e.g. ) et les arêtes aux implications associées aux clauses de la formule. Deux littéraux sont alors dans la même composante fortement connexe du graphe si et seulement si on peut passer de l’un à l’autre et réciproquement via une chaîne d’implications.
Si, pour une variable , les littéraux et sont dans la même composante, cela signifie que la formule est contradictoire. En fait — et ce n’est pas complètement immédiat — cela donne un ensemble de conditions nécessaires et suffisantes pour obtenir la satisfaisabilité.
On pourra lire le chapitre consacré du livre Introduction to Algorithms pour plus de détails.
Étude de la transition satisfaisabilité → frustration
I can’t get no satisfaction
‘Cause I try and I try and I try and I try
— The Rolling Stones
Le programme satisfaction, que j’ai écrit en Rust, permet d’étudier la satisfaisabilité d’instances aléatoires du problème k-SAT lorsque le nombre de clauses augmente.
Plus précisément, considérons le nombre , où désigne le nombre de variables sur lesquelles porte la formule.
Dans le cas d’introduction, on a par exemple puisque l’on a trois clauses et trois variables.
Étudions le pourcentage d’instances satisfaisables sur un échantillon aléatoire lorsque varie.
Problème 2-SAT
Voici ce que l’on obtient pour des formules de taille 2 portant sur 10 variables (l’indication s.p.p correspond au nombre de formules aléatoires générées pour chaque point) :
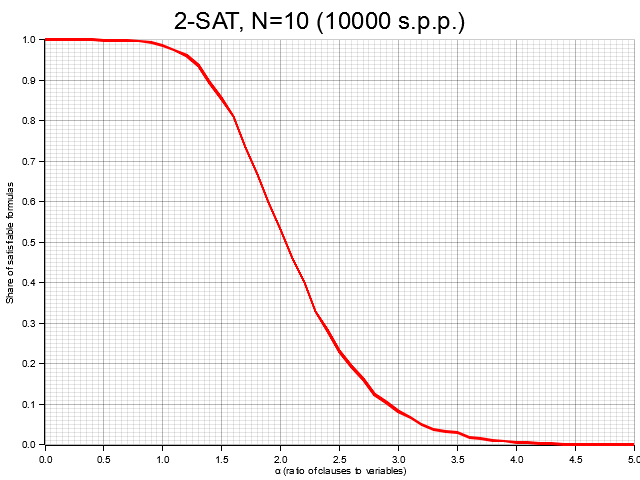
Le taux de formules satisfaisables diminue avec (on s’y attendait), selon une courbe plutôt lisse.
Pour des formules portant sur 1000 variables, l’évolution est beaucoup plus abrupte :
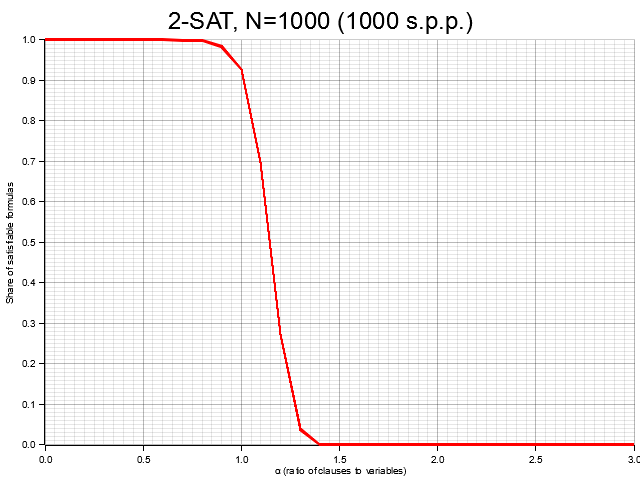
On distingue deux régimes que je nommerai satisfaisabilité et frustration (ce nom sera justifié en dernière partie) :
- Satisfaisabilité : à gauche ( petit), les formules sont presque toutes satisfaisables
- Frustration : à droite ( grand), les formules sont presque toutes non-satisfaisables
Dans le cas limite , ces deux régimes sont séparés strictement par la valeur .
💡 Dans le cas de 2-SAT, il est possible de démontrer l’existence de cette transition et la valeur de . On pourra consulter ce papier pour une preuve, ainsi que celui-ci qui précise le comportement asymptotique.
Problème 3-SAT
Les simulations dans le cas de 3-SAT sont plus lourdes à générer, le problème étant NP-complet.
Pour des valeurs de raisonnables, on peut néanmoins observer aussi une transition de phase. Dans ce cas, on estime qu’elle se situe autour de , mais on a moins de résultats théoriques que pour 2-SAT.
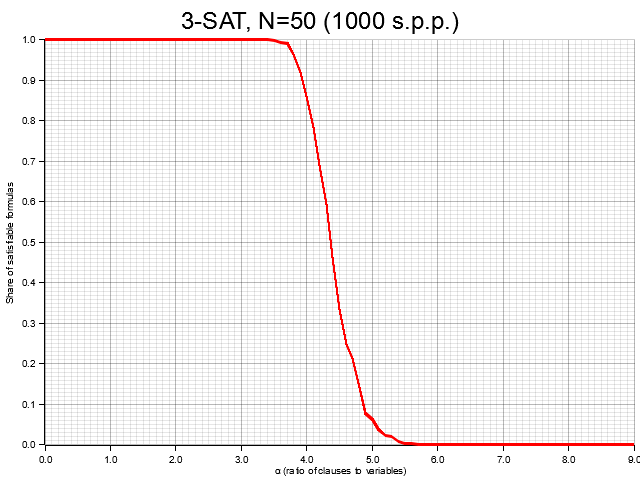
On pourra également consulter le papier Phase transitions and complexity in computer science: an overview qui présente des résultats pour des formules hybrides, comportant des clauses de tailles 2 et 3.
Une approche énergétique de la satisfaisabilité
Considérons à nouveau la formule présentée en introduction : .
Représentons les grandeurs booléennes () par des variable (avec , ).
Dès lors, on peut associer à la formule une fonction « énergie » :
Ainsi définie, je vous laisse vous convaincre que correspond, pour chaque assignation des variables, au nombre de clauses non satisfaites dans la formule.
La satisfaisabilité se traduit alors par la condition que l’énergie minimale accessible soit égale à .
En développant le calcul on obtient .
Cette quantité s’annule lorsque et sont de même signe et de signe opposé : on retrouve la solution proposée en introduction, ainsi que l’alternative correspondant à exclure Pierre et Romane et inviter Quentin.
Lien avec le modèle d’Ising
Plus généralement, une formule 2-SAT va correspondre à une énergie .
C’est la forme générale de l’énergie du modèle d’Ising, les et étant des constantes de couplage.
Le cas le plus classique d’application du modèle d’Ising est la modélisation des propriétés magnétiques de certains matériaux.
Généralement, on considère que le matériau est consitué d’un réseau de petits aimants qui interagissent, chacun avec ses plus proches voisins, selon un terme de couplage constant .
En l’absence de champ magnétique extérieur, l’énergie s’exprime alors simplement .
À basse température, le système va s’arranger de façon à minimiser cette énergie, ce qui conduit à différents comportements selon le couplage.
Dans le cas (ferromagnétisme), les aimants tendent à s’aligner (cliquer sur la grille pour alterner entre les deux variantes) :
| ↑ | ↑ | ↑ | ↑ | ↑ |
| ↑ | ↑ | ↑ | ↑ | ↑ |
| ↑ | ↑ | ↑ | ↑ | ↑ |
| ↑ | ↑ | ↑ | ↑ | ↑ |
| ↑ | ↑ | ↑ | ↑ | ↑ |
Dans le cas (antiferromagnétisme), les aimants tendent à s’opposer à leurs voisins :
| ↓ | ↑ | ↓ | ↑ | ↓ |
| ↑ | ↓ | ↑ | ↓ | ↑ |
| ↓ | ↑ | ↓ | ↑ | ↓ |
| ↑ | ↓ | ↑ | ↓ | ↑ |
| ↓ | ↑ | ↓ | ↑ | ↓ |
Dans les deux cas illustrés ci-dessus, comme dans l’exemple d’introduction, les fonctions d’énergie correspondent à des formules satisfaisables : lorsque l’énergie (totale) est minimale, elle l’est aussi pour chaque terme d’interaction isolé.
Non-satisfaisabilité et frustration magnétique
Considérons la formule suivante :
En développant la fonction d’énergie associée à cette formule, on obtient :
Cette énergie est celle associée à une configuration triangulaire du modèle d’Ising, avec un terme d’interaction antiferromagnétique () :
Comme illustré ci-dessus (cliquer sur le triangle !), il y a six configurations qui minimisent l’énergie de ce système, mais dans chacune d’entre elles au moins deux aimants voisins sont alignés : le système est frustré.
Cette frustration correspond exactement à la non-satisfaisabilité de la formule correspondante.
La vidéo ci-dessous (du centre de recherche ct.qmat) montre une manifestation grandeur nature de la frustration magnétique dans un réseau d’aimants arrangés selon un pavage de Kagomé.
Les systèmes frustrés présentent généralement une multitude d’états d’énergie minimale, ce qui donne lieu à différents phénomènes qui peuvent intéresser les physiciens. Pour approfondir, on pourra lire cette introduction à la physique des systèmes frustrés, par Leticia Cugliandolo.
Vous pouvez commenter cette entrée sur Bluesky, Twitter ou Mathstodon.
N'hésitez pas également à m'envoyer un email (thomas@lipsum.dev).
Maths et applications, avec les mains et avec du code 💻
Suivre sur Twitter