Lipsum.dev

Automates, expressions régulières et arithmétique de Presburger

05 janvier 2024 — Automates, Langages, Logique

L’étude des automates finis (ou machines à états finis) constitue une branche de l’informatique théorique qui trouve de nombreuses applications pratiques.

Une présentation théorique exhaustive serait trop longue pour cet article et je vous renvoie pour cela au très bon livre Automata Theory: An Algorithmic Approach, qui m’a servi de source d’inspiration. Nous allons ici nous focaliser essentiellement sur deux cas d’automates finis qui illustrent des applications possibles.

Dans une première partie, nous évoquerons les expressions régulières et les langages qu’elles permettent de définir.

Dans une seconde partie, nous présenterons une application plus exotique avec un automate fini qui accepte exactement les solutions entières positives de l’équation $2x + 3y \leq 100$ — cette construction fonctionne pour toute formule de l’arithmétique de Presburger.

J’utiliserai la bibliothèque Automathon qui permet de définir simplement des automates finis en Python et de les visualiser graphiquement.

Les expressions régulières

Un modèle-jouet avec Automathon

Un automate fini (déterministe, ce sera le cas par défaut ici) correspond à la donnée de :

Un alphabet $\Sigma$ à partir duquel on va pouvoir constituer les mots que l’on soumettra à l’automate.
Un ensemble fini $Q$ d’états $s_0, s_1, ..., s_n$ .
Une fonction de transition $\delta$ qui indique pour un état donné et un symbole lu (dans l’alphabet $\Sigma$ ), l’état dans lequel l’automate va transitionner.
Un état initial $s_0$ .
Un ensemble d’états finaux, noté $F$ .

Ici, un “mot” doit être compris comme une séquence finie, dans la mesure où une phrase comme “The quick brown fox jumps over the lazy dog” ne constitue qu’un seul mot dans l’alphabet correspondant aux caractères ASCII.

Le fonctionnement est assez simple : l’automate démarre dans l’état $s_0$ et lit un mot $w$ symbole par symbole en effectuant les transitions d’états données par $\delta$ . À la fin du mot, si l’état de l’automate fait partie des états finaux $F$ , le mot est accepté; sinon, il est rejeté.

On peut donc considérer en quelque sorte un automate comme une structure de données — l’automate représente l’ensemble des mots qu’il accepte. Il est d’ailleurs possible d’implémenter diverses opérations ensemblistes sur les automates (e.g. union, intersection, complément, projection), ce qui est utilisé abondamment dans la seconde application que nous présenterons.

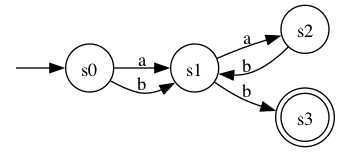
Dans l’exemple ci-dessous, je définis un automate (Deterministic Finite Automata) à quatre états, qui lit des mots sur l’alphabet constitués des deux symboles $a$ et $b$ :

from automathon import DFA
Q = {"s0", "s1", "s2", "s3"}
sigma = {"a", "b"}
delta = {
    "s0": {
        "a": "s1",
        "b": "s1",
    },
    "s1": {
        "a": "s2",
        "b": "s3",
    },
    "s2": {
        "b": "s1",
    },
    "s3": {}
}
automata = DFA(Q=Q, sigma=sigma, delta=delta, initialState="s0", F={"s3"})

Testons l’acceptation de certains mots :

>>> automata.accept("abba")
False
>>> automata.accept("aabababb")
True

La définition d’un automate n’est pas forcément très lisible, mais il est possible de le représenter graphiquement :

>>> automata.view("ab-DFA")

On obtient le diagramme ci-dessous, où l’état initial est représenté tout à gauche avec une flèche vide entrante et où l’état final est entouré d’un double cercle :

En lisant ce diagramme, on comprend mieux le fonctionnement de cet automate : un mot est accepté s’il commence par un a ou un b, suivi éventuellement par une succession de ab, puis par un b.

Expressions régulières formelles

On peut utiliser la notation (a|b)(ab)*b pour désigner le langage accepté par cet automate, une telle notation étant ce qu’on appelle en informatique théorique une expression régulière formelle (nous reviendrons plus loin sur la distinction avec les expressions régulières usuelles).

C’est le mathématicien Stephen Cole Kleene qui a introduit ce concept dans les années 50 et montré que les langages définis par des expressions régulières étaient ceux reconnus par des automates finis : on parle de langages réguliers (ou rationnels).

Étant donnée une expression régulière, il existe différents algorithmes permettant de construire un automate acceptant exactement les mêmes mots (on parlera de “compilation” de l’expression régulière). De même, la construction inverse est possible : étant donné un automate fini, on construit une expression régulière qui détermine le même langage que cet automate. Ces deux constructions sont décrites précisément dans le livre cité en introduction.

Notons que la compilation d’une expression régulière passe généralement par la construction intermédiaire d’un automate fini non déterministe, structure d’automate plus générale que celle présentée ici.

💡 Un exemple de langage non régulier

Il existe des langages qui ne peuvent pas être reconnus par un automate fini — ou, ce qui est équivalent, qui ne peuvent pas être définis par une expression régulière.

Je ne souhaite pas développer spécifiquement la théorie des langages ici, mais il est assez simple de se convaincre que le langage construit à partir des symboles de parenthèses "(" et ")" et constitué exclusivement des mots bien parenthésés n’est pas régulier.

Un mot comme "((()))()" est bien parenthésé : on peut faire correspondre bijectivement à chaque parenthèse ouvrante "(" une parenthèse fermante ")" qui se trouve à sa droite. Un mot comme "())(" n’est pas bien parenthésé : la parenthèse ")" en troisième position ne ferme aucune parenthèse ouverte.

Si un automate à états finis reconnaissait le langage des mots bien parenthésés, il faudrait qu’il ait des états différents après avoir lu les préfixes w0 = "", w1 = "(", w2 = "((", w3 = "(((", etc. et donc qu’il ait une infinité d’états possibles. Il est cependant possible de reconnaître ce langage avec un automate à pile.

Expressions régulières en pratique

En pratique, les langages de programmation introduisent généralement une syntaxe plus riche pour définir les expressions régulières. Par exemple, en Python :

re.match("^[ab](ab)*b$", "aabababb")   # equivalent to formal regex (a|b)(ab)*b

Si la plupart de ces différences syntaxiques impactent surtout la forme (ces expressions restent représentables par des automates finis), le langage Perl a introduit dans les années 80 de nouvelles fonctionnalités comme les références arrières (backreferences), incompatibles avec le formalisme théorique décrit précédemment. Ceci peut impacter significativement les performances : un automate fini vérifie un mot en un temps proportionnel à la longueur du mot, ce n’est plus aussi simple avec les références arrières.

Pour cette raison, certains moteurs d’expressions régulières comme celui de Rust n’implémentent pas ces fonctionnalités non standard.

Pour en savoir plus, je vous invite à lire cet article qui revient sur l’historique du développement des expressions régulières.

Algorithme de décision de l’arithmétique de Presburger

Dans ce papier, une procédure permettant de construire un automate fini à partir de certaines équations arithmétiques est présentée : l’Automate construit accepte les séquences qui encodent des solutions de l’équation.

Par exemple, nous verrons plus loin un automate fini qui accepte les couples $(x, y)$ solutions de l’équation $2x + 3y \leq 100$ et uniquement ceux-ci.

Je ne souhaite pas détailler ici l’ensemble de cette procédure : c’est précisément ce que fait ce papier et vous pourrez le lire pour plus de détails. J’aimerais simplement souligner quelques aspects intéressants des points de vue algorithmique et mathématique.

Arithmétique de Presburger

Les formules pour lesquelles la procédure produit un automate fini sont celles de l’arithmétique de Presburger. Elle consiste en une formalisation des entiers naturels et des règles de calcul sur ceux-ci à l’exclusion de la multiplication.

On ne considère donc que des formules constituées à partir de nombres entiers positifs, de symboles de variables ( $x, y, z, ...$ ), du symbole d’égalité $=$ , des symboles logiques $\exists, \forall, \lnot, \land, \lor$ et du symbole d’addition $+$ .

La formule $\varphi := \exists z, 2x + 3y + z = 100$ est un exemple de formule de l’arithmétique de Presburger, portant sur les deux variables libres $x$ et $y$ . Elle est équivalente à la formule $\psi := 2x + 3y \leq 100$ puisque la variable $z$ liée au quantificateur existentiel dans $\varphi$ représente un entier positif.

💡 Mojżesz Presburger a étudié cette théorie arithmétique en 1929 (voir ici pour une traduction de l’article d’origine) et prouvé qu’elle était décidable algorithmiquement, d’une toute autre façon que celle présentée ici qui utilise les automates.

Opérations ensemblistes sur les automates finis

Le papier présente différentes opérations sur les automates qui vont correspondre à certaines constructions logiques, par exemple :

Le complément est une construction qui à partir d’un automate fini $A$ produit un automate $A^c$ qui accepte un mot si et seulement si $A$ le rejette. Cette construction est utile pour construire l’automate correspondant à une formule $\lnot \varphi$ à partir de celui correspondant à la formule $\varphi$ .
L’union (ou produit) de deux automates est une construction utilisée ici pour obtenir un automate correspondant à une formule $\varphi_1 \lor \varphi_2$ à partir de deux automates correspondant à $\varphi_1$ et $\varphi_2$ .
La projection est une opération décrite précisément dans le livre cité en introduction et utilisée dans le papier pour construire un automate correspondant à la formule $\exists x, \varphi(x, y)$ à partir d’un automate associé à une formule $\varphi(x,y)$ .

À l’aide des différentes opérations et d’automates particuliers reconnaissant les égalités $a_0 x_0 + ... + a_{n-1} x_{n-1} = b$ (procédure EQtoDFA dans le papier), une formule quelconque à $n$ variables libres de l’arithmétique de Presburger est transformée en un automate reconnaissant les solutions $(x_0, ... x_{n-1})$ . Le cas d’une formule close ( $n = 0$ ) donnera un automate à un seul état : la formule est acceptée si c’est un état final.

Un exemple

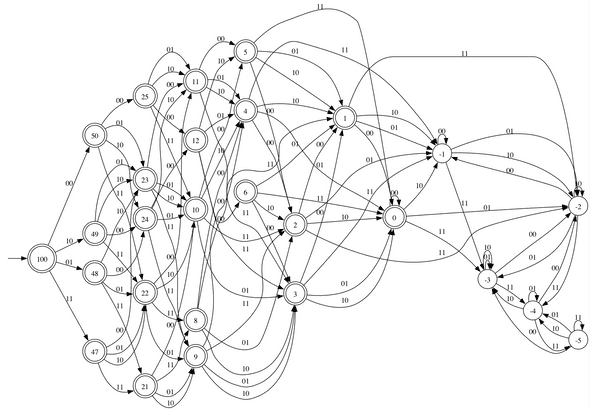
J’ai implémenté ci-dessous l’algorithme INEQtoDFA décrit dans le papier pour construire un automate correspondant à l’inégalité $2x + 3y \leq 100$ :

def ineq_to_dfa(A: list[int], b: int) -> DFA:
    n = len(A)
    Q = set()
    sigma = {bin(i)[2:].zfill(n) for i in range(2**n)}
    delta = defaultdict(dict)
    F = set()
    W = {b}
    while W:
        k = W.pop()
        Q.add(k)
        if k >= 0:
            F.add(str(k))
        for s in sigma:
            j = floor((k - sum(a * int(d) for a, d in zip(A, s))) / 2)
            if j not in Q:
                W.add(j)
            delta[str(k)][s] = str(j)
    # authomaton.DFA requires states to be strings
    return DFA({str(q) for q in Q}, sigma, delta, str(b), F)
A = [2, 3]
b = 100
automata = ineq_to_dfa(A, b)

Voici le diagramme correspondant à cet automate à 27 états :

Comme visible sur les transitions de l’automate, on utilise un codage binaire pour représenter un couple d’entiers. Les paires de chiffres correspondant à $x$ et $y$ sont envoyées successivement à l’automate en commençant par le poids faible, par exemple (le code complet est disponible ici) :

>>> encode(23, 16)
['10', '10', '10', '00', '11']

On vérifie alors :

>>> automata.accept(encode(23, 16))
True    # 2 * 23 + 3 * 16 = 94 <= 100
>>> automata.accept(encode(33, 28))
False   # 2 * 33 + 3 * 28 = 150 > 100

Maths et applications, avec les mains et avec du code 💻
Suivre sur Twitter