Théorie des corps, continu et discret

11 novembre 2023 — Logique, Théorie des corps, Transfert

On distingue parfois en mathématiques deux concepts que sont les mathématiques continues et les mathématiques discrètes.

Le corps des nombres réels $\Bbb{R}$ et son extension $\Bbb{C}$ sont des exemples typiques d’objets continus.

D’un autre côté, le discret s’intéresse aux ensembles finis ou dénombrables. Cela concerne par exemple l’arithmétique ou le formalisme utilisé pour étudier théoriquement l’informatique — les ordinateurs manipulent des objets représentés par des entiers.

L’utilisation des courbes elliptiques en cryptographie est un exemple intéressant à cet égard : la notion de courbe est issue de considérations liées au continu et les outils pour les étudier sont historiquement ceux du calcul infinitésimal. Pourtant, ce même type de formalisme est mis en œuvre en cryptographie dans un cadre par nature fini — on pourra lire cette entrée qui présente un usage des courbes elliptiques en cryptographie.

Dans cet article, nous allons faire appel à des considérations du domaine de la logique, pour montrer comment certains résultats exprimés dans la théorie des corps peuvent se transférer d’un cadre continu à un cadre discret (et vice versa).

Théorie des corps

La théorie des corps vise à extraire un langage et des propriétés qu’ont en commun des structures comme les nombres rationnels, les nombres réels ou les nombres complexes.

On peut alors énoncer des propositions et tenter de les prouver à l’aide des axiomes de la théorie et des règles d’inférence de la logique — ce qui revient en pratique à effectuer des manipulations sur des phrases mathématiques, sans qu’il soit nécessaire de leur donner un sens particulier.

Les théorèmes démontrés dans ce cadre s’appliqueront alors à toute structure vérifiant les axiomes de la théorie.

💡 Dans tout cet article, le mot théorie est employé au sens de la logique du premier ordre. J’avais déjà abordé ce sujet dans un article au sujet des théories arithmétiques, j’essaierai néanmoins de ne pas supposer trop de prérequis.

La théorie des corps introduit des symboles de constantes $0$ et $1$, des symboles de fonction $+, -, \times$ et les axiomes suivants :

1. $0 \neq 1$
2. $\forall x \forall y \forall z (x + (y + z) = (x + y) + z)$
3. $\forall x \forall y (x + y = y + x)$
4. $\forall x (x + 0 = x)$
5. $\forall x (x + (-x) = 0)$
6. $\forall x \forall y \forall z (x \times (y \times z) = (x \times y) \times z)$
7. $\forall x \forall y (x \times y = y \times x)$
8. $\forall x (x \times 1 = x)$
9. $\forall x (x \neq 0 \implies \exists y, x \times y = 1)$
10. $\forall x \forall y \forall z (x \times (y + z) = (x \times y) + (x \times z))$

Un corps est un modèle de cette théorie, c’est-à-dire une structure $(K, 0, 1, +, -, \times)$ telle que :

• $K$ est un ensemble
• $0$ désigne un élément de $K$
• $1$ désigne un élément de $K$
• $+, -, \times$ sont des fonctions (de $K \times K$ dans $K$)
• les axiomes ci-dessus, interprétés dans cette structure, sont vrais

Il est bien connu que $\Bbb{Q}$, $\Bbb{R}$ ou $\Bbb{C}$ sont des corps — ils sont d’ailleurs à l’origine de la formalisation de ce concept. Ils vérifient $\Bbb{Q} \subset \Bbb{R} \subset \Bbb{C}$ et une telle séquence d’extensions de corps est parfois appelée une tour.

Les corps finis

Si $p$ est un nombre premier, on peut construire un corps fini de taille $p$ en considérant le calcul dans les entiers modulo $p$ — ceci est essentiellement une conséquence de l’identité de Bézout. Le corps ainsi obtenu est noté $F_p$ et vérifie en particulier l’égalité ${\underbrace{1 + 1 + ... + 1}_{\text{p fois}} = 0}$ : $F_p$ est de caractéristique $p$.

De façon générale, pour tout entier $n \geq 1$ et en notant $q = p^n$, il existe un unique corps fini $F_q$ de taille $q$. $F_q$ est une extension de $F_p$ que l’on peut construire comme corps de décomposition du polynôme $X^q - X$, ce qui revient (très sommairement) à introduire successivement des racines de ses facteurs irréductibles.

Il s’agit du même type de procédé (on parle d’extension algébrique) qui permet de construire $\Bbb{C}$ à partir de $\Bbb{R}$ en ajoutant une racine $i$ au polynôme $X^2 + 1$. Dans le cas de $\Bbb{C}$, le corps obtenu est algébriquement clos et il est impossible de réitérer le processus.

Le corps $F_q$ lui est fini, et il est toujours possible de trouver un nouveau polynôme irréductible de degré $d \geq 2$ et ainsi de construire une nouvelle extension (ce qui donne dans ce cas $F_{q^d}$).

On peut par exemple obtenir une tour d’extensions $F_p \subset F_{p^2} \subset ... \subset F_{p^{n!}}$ que l’on peut faire croître indéfiniment (j’ai choisi d’utiliser la factorielle car $F_{p^a} \subset F_{p^b} \iff a | b$, ce qui résulte essentiellement des propriétés des polynômes $X^q - X$ mentionnés plus haut).

On peut associer à cette construction un ensemble limite noté $\overline{F_p} = \bigcup_{n \geq 1}{F_{p^n}}$ qui est infini dénombrable.

Par ailleurs, si $P$ est un polynôme à coefficients dans $\overline{F_p}$, il existe $n \geq 1$ tel que les coefficients de $P$ soient tous dans $F_{p^n}$. Si $Q$ est un facteur irréductible de degré $d$ de $P$ dans $F_{p^n}$, $Q$ admet une racine dans $F_{p^{nd}} \subset \overline{F_p}$. On en déduit que $\overline{F_p}$ est un corps algébriquement clos.

💡 En toute rigueur, la construction de $\overline{F_p}$ utilise la notion de limite inductive. Notez qu’il est tout à fait possible de représenter informatiquement et de façon exacte les éléments de $\overline{F_p}$ : on pourra lire par exemple Standard Generators of Finite Fields and their Cyclic Subgroups.

Théorie des corps algébriquement clos

Comme je le mentionnais plus haut, c’est un résultat bien connu que dans $\Bbb{C}$, tout polynôme non constant admet au moins une racine. Il en existe une multitude de preuves qui, d’une façon ou d’une autre, font toutes appel à des propriétés topologiques correspondant à l’idée que $\Bbb{R}$ (et par extension $\Bbb{C}$) n’a « pas de trou ».

Le résultat en lui-même n’est pas propre à $\Bbb{C}$ — on peut toujours construire la clôture algébrique d’un corps, comme $\overline{F_p}$ — et s’exprime bien dans le langage de la théorie des corps.

La théorie des corps algébriquement clos étend la théorie des corps en y ajoutant pour chaque $n \geq 1$, l’axiome ${\forall a_0 ... \forall a_{n-1} \exists x (x^n + a_{n-1} x^{n-1} + ... + a_0 = 0)}$.

Élimination des quantificateurs

La formule suivante (dans laquelle $a, b, c, d$ désignent des variables libres) peut se déduire des axiomes de la théorie des corps :

$(\exists x \exists y, \lnot(x = 0 \land y = 0) \land ax + by = 0 \land cx + dy = 0) \iff ad - cb = 0$

Cette formule correspond à un résultat classique d’algèbre linéaire, caractérisant l’existence de zéros non triviaux d’un système linéaire en fonction du déterminant de celui-ci.

Il s’agit d’une équivalence entre les formules (portant sur quatre variables libres) $\varphi$ et $\psi$ suivantes :

• $\varphi := \exists x \exists y, \lnot(x = 0 \land y = 0) \land ax + by = 0 \land cx + dy = 0$
• $\psi := ad - cb = 0$

La formule $\varphi$ est une formule quantifiée : elle comporte deux variables $x, y$ liées par des quantificateurs existentiels $\exists$. La formule $\psi$ ne comporte quant à elle aucun quantificateur : on dit qu’on a éliminé les quantificateurs de $\varphi$.

Il est impossible, dans le cadre de la théorie des corps, d’éliminer les quantificateurs de la formule $\exists x, x^2 + 1 = 0$ — comme nous le justifierons plus loin, cela impliquerait la décidabilité de cette formule en caractéristique zéro, qui aurait alors même valeur de vérité dans $\Bbb{R}$ et $\Bbb{C}$.

En revanche, dans la théorie des corps algébriquement clos, cette formule est un théorème et en particulier on peut en éliminer le quantificateur : ${(\exists x, x^2 + 1 = 0) \iff \top}$ (symbole logique signifiant vrai, par opposition à $\bot$).

Dans l’exemple ci-dessous, nous utilisons le discriminant $\Delta = 2^2 - 4 \cdot 3 \cdot 5$ du polynôme $P = 3 X^2 + 2 X + 5$ pour éliminer les quantificateurs d’une formule signifiant que $P$ admet (au moins) deux racines distinctes :

En fait, et c’est là un résultat remarquable, la théorie des corps algébriquement clos admet l’élimination des quantificateurs : pour toute formule quantifiée qu’elle est capable d’exprimer, il existe une formule équivalente sans quantificateurs.

Mieux encore, on peut décrire un algorithme qui va effectuer cette transformation : cet algorithme prend en entrée une formule $\varphi$ quantifiée et, en utilisant les axiomes de la théorie des corps algébriquement clos, transforme cette formule en une formule équivalente $\psi$ sans quantificateurs.

Un algorithme d’élimination des quantificateurs

L’article A formal quantifier elimination for algebraically closed fields décrit une façon de procéder.

Les points clefs de ce procédé, résumés de façon très sommaire (il faudra lire l’article si vous voulez en savoir plus), sont :

• Mise sous forme prénexe de la formule $\varphi$ pour obtenir une formule équivalente dont tous les quantificateurs sont regroupés à gauche.
• Utilisation de l’équivalence $\forall x, A \iff \lnot(\exists x, \lnot A)$ pour éliminer les quantificateurs universels $\forall$.
• Tant qu’il reste un quantificateur existentiel $\exists$ dans la formule :
  • Mise sous forme normale disjonctive de la partie de droite (après les quantificateurs) et distribution du dernier symbole $\exists$ dans chaque formule de la disjonction : $\exists x, A \lor B \iff (\exists x, A) \lor (\exists x, B)$.
  • Utilisation des axiomes de la théorie des corps pour transformer les formules résultantes (les $\exists x, A$ ci-dessus) en formules de la forme $\exists x, P(x)$ où $P$ est une expression polynomiale en $x$. C’est la partie la plus subtile, $A$ pouvant désigner une conjonction quelconque d’égalités et inégalités polynomiales. L’algorithme utilise notamment une variante de la division euclidienne des polynômes.
  • Utilisation des axiomes de la théorie des corps algébriquement clos pour transformer une formule du type $\exists x, P(x)$ en une formule non quantifiée portant sur les coefficients de $P$ (e.g. $\exists x, a x^2 + 1 = 0 \iff a \neq 0$).

L’élimination des quantificateurs telle que décrite ici s’applique à toute formule, avec ou sans variable libre. Dans le cas d’une proposition (formule sans variable libre), la formule $\psi$ résultant de l’élimination des quantificateurs n’a plus aucune variable (libre ou liée).

Après simplification, et comme dans l’exemple étudié précédemment (cas du discriminant), les atomes de la proposition résultante sont alors de la forme $p = 0$ (on utilise abusivement un nombre premier $p$ pour désigner l’expression $\underbrace{1 + 1 + ... + 1}_{\text{p fois}}$).

Décidabilité et complétude

Une proposition $P$ est dite décidable dans une théorie si $P$ ou sa négation $\lnot P$ est démontrable dans cette théorie.

Une théorie dont toutes les propositions sont décidables est dite complète.

Par exemple, $\exists x, x^2 + 1 = 0$ n’est pas une proposition décidable de la théorie des corps, mais c’est une proposition décidable de la théorie des corps algébriquement clos.

La proposition $1 + 1 = 0$ n’est en revanche pas décidable dans la théorie des corps algébriquement clos — elle est fausse dans $\Bbb{C}$ mais vraie dans $\overline{F_2}$.

Ceci nous montre qu’aucune de ces deux théories n’est complète.

Théorie des corps algébriquement clos de caractéristique $p$

Pour tout nombre premier $p$, notons $\sigma_p$ la proposition ${\underbrace{1 + 1 + ... + 1}_{\text{p fois}} = 0}$.

La théorie des corps algébriquement clos de caractéristique 0 est la théorie obtenue en ajoutant les axiomes $\lnot \sigma_p$, pour tout nombre premier $p$, à la théorie des corps algébriquement clos.

Pour un nombre premier $p$ fixé, la théorie des corps algébriquement clos de caractéristique $p$ est la théorie obtenue en ajoutant l’axiome $\sigma_p$ à la théorie des corps algébriquement clos.

Ces théories sont complètes : par élimination des quantificateurs (dans la théorie des corps algébriquement clos), toute proposition $\varphi$ se ramène à une proposition équivalente $\psi$ constituée d’atomes $\sigma_p$ reliés par des connecteurs logiques. Une fois la caractéristique fixée, la valeur de vérité de chacun de ces atomes est entièrement déterminée et $\psi$ peut alors être évaluée, par exemple par un algorithme.

Théorème de transfert

Étant donnée une proposition $\varphi$ de la théorie des corps, on a vu que pour toute caractéristique $p$ (ici $0$ ou un nombre premier), $\varphi$ est décidable dans la théorie des corps algébriquement clos de caractéristique $p$ : c’est la complétude.

Notons $V_{\varphi}(p) = 1$ si $\varphi$ est un théorème, $V_{\varphi}(p) = 0$ si $\lnot \varphi$ est un théorème (de la théorie des corps algébriquement clos de caractéristique $p$).

Par élimination des quantificateurs, on obtient une proposition $\psi$ équivalente (dans la théorie des corps algébriquement clos) comportant un nombre fini d’atomes $\sigma_p$.

Notons $p_0$ le plus petit nombre premier majorant strictement les nombres premiers intervenant dans ces atomes de $\psi$.

Pour $p \geq p_0$, la valeur de vérité des atomes ne change plus : $V_{\varphi}(p) = V_{\varphi}(p_0)$ et de même $V_{\varphi}(0) = V_{\varphi}(p_0)$.

Par complétude, en considérant des cas particuliers de corps algébriquement clos pour chaque caractéristique, on en déduit le théorème de transfert ci-dessous.

Étant donné une proposition $\varphi$ de la théorie des corps, on a équivalence entre :

1. $\varphi$ est un théorème de la théorie des corps algébriquement clos de caractéristique $0$
2. $\varphi$ est vraie dans $\Bbb{C}$
3. Il existe $p_0$ premier tel que $\varphi$ est vraie dans $\overline{F_p}$ pour $p \geq p_0$

Applications

On désigne parfois sous le nom de principe de Lefschetz l’équivalence entre les points (1) et (2) ci-dessus. Ce principe permet de justifier que certains résultats algébriques obtenus sur $\Bbb{C}$, par exemple avec les outils de l’analyse complexe ou de la topologie, se généralisent à tout corps algébriquement clos de caractéristique 0.

L’équivalence avec le point (3) nous permet également d’obtenir le résultat pour des caractéristiques « suffisamment grandes » — pour une formule $\varphi$ donnée, on peut être plus précis en éliminant les quantificateurs pour expliciter des conditions sur la caractéristique $p$.

Courbes elliptiques

Les courbes elliptiques sont des courbes associées à certaines équations algébriques et sur lesquelles on peut définir une loi de groupe commutatif.

Les outils de l’analyse complexe et en particulier l’étude des fonctions elliptiques comme la fonction ℘ de Weierstrass permettent de faire apparaître naturellement le concept de courbe elliptique et la loi de groupe associée dans le cas complexe.

Dans ce cas, la loi de groupe correspond, à un isomorphisme près, à l’addition des points sur un tore (voir l’article Wikipedia).

Il est possible (mais fastidieux) de formuler certaines des propriétés de cette loi de groupe dans la théorie des corps et d’étendre, par transfert, leur validité à d’autres corps algébriquement clos.

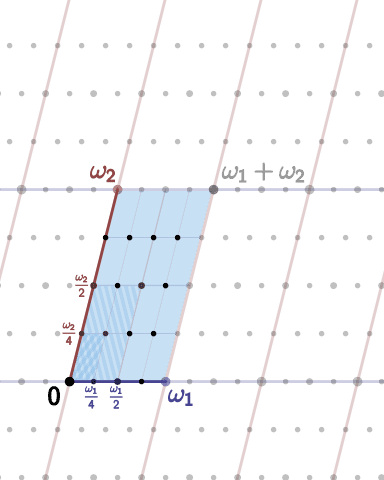
L’image ci-dessus met en évidence (dans le cas $n=4$) le fait que le sous-groupe des points d’ordre $n$ d’une courbe elliptique complexe est de cardinal $n^2$. Ce résultat se transfère à certaines caractéristiques $p > 0$ et est fondamental dans la compréhension de certains vecteurs d’attaque de la cryptographie sur courbes elliptiques. Cet exemple est mentionné en page 10 de la présentation The group structure of rational points of elliptic curves over a finite field de Damien Robert.

Le théorème d’Ax-Grothendieck

Ce théorème affirme que pour tout entier naturel $n$, si $f$ est une fonction polynomiale de ${\Bbb{C}}^n$ dans ${\Bbb{C}}^n$ (chacune de ses fonctions coordonnées est un polynôme en $n$ variables) injective, alors $f$ est surjective.

Nous allons le montrer dans le cas $n=2$ et pour des polynômes de degré au plus $2$. La proposition correspondante, qui comme nous allons le voir est déjà assez complexe, illustre le procédé qui restera valable pour tout $n$ et tout majorant du degré.

Si je n’ai pas fait d’erreur, la proposition $\varphi$ suivante de la théorie des corps exprime le résultat recherché pour les fonctions de cette forme :

Par ailleurs :

• $\varphi$, interprétée dans un corps fini $F_q$, est vraie : une fonction d’un ensemble fini dans lui-même est injective si et seulement si elle est surjective.
• $\varphi$, interprétée dans $\overline{F_p}$, est vraie : Fixons les coefficients de $f$ et un sous-corps fini $F_q$ de $\overline{F_p}$ contenant tous ces coefficients et supposons $f$ injective sur $\overline{F_p}$. $f$ est en particulier injective — et donc surjective par ce qui précède — sur $F_q$. $\overline{F_p}$ étant par construction l’union de tels corps finis, $f$ est surjective sur $\overline{F_p}$.

Par le théorème de transfert (ici (3) ⇒ (2)), on en déduit que $\varphi$ est vraie dans $\Bbb{C}$.

Cet exemple est tiré d’un article d’Élisabeth Bouscaren sur la théorie des modèles publié dans la gazette de la SMF. Cet article utilise la notion d’ultraproduit pour établir le théorème de transfert mentionné plus haut, ce qui permet d’obtenir des résultats de portée plus générale. L’approche ad hoc développée ici a le mérite de ne pas nécessiter trop de formalisme et de décrire un algorithme permettant l’élimination des quantificateurs dans le cas des corps algébriquement clos.

---

Vous pouvez commenter cette entrée sur Bluesky, Twitter ou Mathstodon.
N'hésitez pas également à m'envoyer un email (thomas@lipsum.dev).

---

• ← Qu'est-ce qu'un assistant de preuve ?
• Automates, expressions régulières et arithmétique de Presburger →