Autour des harmoniques sphériques
21 mai 2023 — Harmoniques sphériques, Physique, 3D
Les séries de Fourier permettent de décomposer une fonction périodique en somme de composantes, les harmoniques, correspondant aux multiples entiers d’une même fréquence, la fondamentale.
Les harmoniques sphériques, auxquelles nous allons nous intéresser, permettent une décomposition similaire des fonctions définies sur une sphère.
J’aimerais présenter ici une sélection de quelques applications de ces harmoniques sphériques, en informatique et en physique.
Pour une bonne compréhension, cela nécessite un peu de formalisme mathématique que j’introduirai au fil de l’article — vous pouvez sauter ces parties et vous y référer si besoin.
Les séries de Fourier permettent de décomposer une fonction (définie sur le cercle unité , ou de façon équivalente -périodique), en somme de composantes :
où les sont des complexes et .
De façon analogue, les harmoniques sphériques ( constituent une base orthonormée de l’espace hermitien des fonctions complexes de carré sommable sur la sphère unité .
Ces fonctions sont généralement exprimées en coordonnées sphériques — leur expression exacte importe peu pour l’instant.
Une fonction définie sur la sphère se décompose donc comme une somme , parfois appelée (en physique notamment) son développement multipolaire.
Étant donnée une telle fonction , on obtient le coefficient par un produit scalaire, ici une intégrale sur la surface de la sphère :
Ce préambule mathématique étant posé, voyons comment elles peuvent être utilisées.
Les light probes
L’incrustation d’objets fictifs dans des scènes de films pour créer des effets spéciaux nécessite de capter la lumière atteignant cet objet selon toutes les directions, afin de pouvoir la restituer au rendu.
Historiquement, des sondes — les light probes — sous forme de sphères plus ou moins réfléchissantes étaient utilisées à cet effet.
Dans le monde du rendu 3D, ce terme désigne aujourd’hui un enregistrement de la lumière parvenant à un point selon toutes les directions possibles, il s’agit donc pour chaque couleur d’encoder une fonction définie sur la sphère unité.
Pour cela, il est commun d’utiliser un développement multipolaire de limité aux 9 premiers coefficients :
- le coefficient correspondant à — terme monopolaire
- les 3 coefficients correspondant à — terme dipolaire
- les 5 coefficients correspondant à — terme quadrupolaire
Par exemple, c’est ainsi que sont encodées les LightProbes du moteur 3D Unity.
La valeur de ces coefficients — l’intégrale indiquée en préambule — peut être évaluée par échantillonnage selon la méthode de Monte Carlo.
Cette représentation sous forme d’harmoniques sphériques est pratique pour plusieurs raisons :
- les termes éliminés correspondent à de grandes valeurs de et donc à des détails plus fins (on pourra faire l’analogie avec la compression JPEG)
- certains calculs, impliquant notamment la réflectivité bidirectionnelle des surfaces, font intervenir des produits scalaires qui s’expriment simplement à partir des coefficients du développement
- cette représentation ne privilégie aucune direction (ce point, plus subtil, sera précisé dans le dernier paragraphe)
Ci-dessus, utilisation des harmoniques sphériques pour reconstruire l’éclairage ambiant en réalité augmentée (framework ARCore de Google). Pour en savoir plus sur l’utilisation des harmoniques sphériques pour le rendu lumineux, vous pouvez lire l’article Spherical Harmonics Lighting: the Gritty Details.
Étude du champ magnétique terrestre
Le champ magnétique terrestre résulte de courants électriques générés dans le noyau externe par des mouvements de métaux liquides.
Au-dessus de la surface de la Terre, on peut considérer que les équations de Maxwell donnent pour le champ magnétique :
D’où l’existence d’un potentiel scalaire tel que et (◇).
À ce stade, il est nécessaire que je vous en dise un peu plus sur les harmoniques sphériques et leur relation avec l’opérateur qui apparaît ci-dessus (noté ), le laplacien.
Ce qui suit ne sera pas complètement rigoureux, mais aidera je l’espère à comprendre la suite.
Cas unidimensionnel
Si l’on considère l’espace , on peut définir un opérateur par .
Je vous laisse montrer que l’on a pour :
- ( est un opérateur Hermitien)
- ( est négatif)
Indice : utiliser des intégrations par parties
Sous certaines conditions, que je ne développerai pas mais qui sont respectées dans ce cas (voir ici), un opérateur Hermitien est diagonalisable dans une base orthonormée.
En l’occurrence, est diagonalisable dans la base de Fourier des définis en introduction et l’on a .
Cas tridimensionnel
L’opérateur est le laplacien : .
Il s’exprime en coordonnées sphériques par :
L’opérateur qui apparaît ici s’applique aux fonctions définies sur la sphère.
On montre qu’il s’agit d’un opérateur Hermitien négatif (l’opérateur de Laplace-Beltrami sur la sphère).
Il est diagonalisable dans la base des harmoniques sphériques et l’on a .
Sachant cela, je vous laisse vérifier que les fonctions ci-dessous (où les sont des complexes quelconques) sont solutions de (◇):
En pratique, le potentiel est une grandeur physique (réelle, associée à un champ qui s’annule à l’infini). Son expression est de la forme :
On introduit le rayon terrestre de façon à avoir des coefficients , homogènes à un champ magnétique (en teslas).
Les polynômes sont les polynômes associés de Legendre qui interviennent dans l’expression des harmoniques sphériques.
Quelques remarques :
- on a , de sorte que chaque composante d’ordre est bien caractérisée par coefficients
- il n’y a pas de terme monopolaire (), qui correspondrait à un monopôle magnétique
Le référentiel IGRF
Le référentiel IGRF maintient une table de valeurs pour les paramètres , , qui est établie à partir de relevés sur Terre ou dans l’espace.
Des missions spatiales comme Swarm ont permis dans les dernières décennies d’estimer ces paramètres jusqu’à (195 coefficients !).
En pratique, le terme dipolaire () domine largement le développement multipolaire et le champ magnétique terrestre peut en première approximation être considéré comme dipolaire.
Des librairies logicielles (par exemple celle-ci en Python) utilisant les données IGRF permettent de recalculer le champ magnétique en un point donnée :
>>> pyIGRF.igrf_value(48.8566, 2.3522)(-1.233314780986759,64.33720132677418,20676.52712529564,20671.737148176166,-445.0362230200669,43034.13302220379,47743.6422881185)
Ici, j’apprends que le champ magnétique à Paris vaut environ 47743 nT et que sa déclinaison (l’erreur angulaire entre l’indication de direction d’une boussole et le vrai pôle Nord) est d’environ -1.23˚.
En pratique, le champ magnétique terrestre évolue avec le temps, notamment ses composantes d’ordre , et le pôle Nord magnétique se déplace. Pour en savoir plus, je vous invite à lire International Geomagnetic Reference Field: the thirteenth generation .
Mécanique quantique et moment cinétique
En mécanique quantique, l’état d’un système physique est encodé par un vecteur d’un espace de Hilbert, par exemple une fonction d’onde.
Les observables correspondent à des opérateurs Hermitiens sur cet espace et les résultats des mesures sont des valeurs propres (qui sont réelles) de ces opérateurs.
La mesure s’interprète alors en terme probabiliste : la probabilité de mesurer la valeur pour l’observable est donnée par où désigne le projecteur orthogonal sur le sous-espace propre associé à la valeur propre de et où on a utilisé la notation bra-ket pour le produit scalaire.
Le Hamiltonien est l’opérateur correspondant à l’énergie d’un système.
Dans le cas d’un système à deux corps en interaction — par exemple une molécule diatomique, ou le couple proton-électron d’un atome d’hydrogène — on peut modéliser le système par une fonction d’onde (en utilisant le formalisme de la masse réduite).
On s’intéresse alors au moment cinétique, dont les composantes sont données par les opérateurs , , , ainsi qu’à son carré .
Sous condition d’invariance par rotation du Hamiltonien, , et commutent et on cherche alors à les diagonaliser dans une base commune.
On trouve ainsi des fonctions propres de la forme (♤), la relation expliquant l’apparition naturelle des harmoniques sphériques : .
Atome d’hydrogène
Dans le cas de l’atome d’hydrogène, l’équation aux valeurs propres fait intervenir un terme d’interaction coulombienne en et sa résolution fait apparaître des états caractérisés par trois nombres quantiques : le premier quantifie la fonction de l’expression (♤), les deux derniers désignent quant à eux l’harmonique sphérique intervenant dans ce produit.
La description complète de l’état du système nécessite néanmoins de prendre en compte une autre observable, le spin, que nous n’avons pas évoqué ici.
Cas d’une molécule diatomique ()
Dans le cas d’une molécule diatomique, sous certaine conditions, il est possible d’observer l’énergie rotationnelle du système et de mettre en évidence expérimentalement le spectre de .
On observe par exemple ci-dessous des pics dont l’espacement en fréquence est proportionnel à :
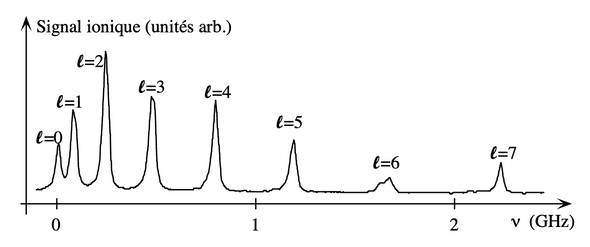 Mise en évidence de la quantification du carré du moment cinétique dans le cadre d’une expérience avec des molécules froides de éclairées par un laser de fréquence variable.
Cette expérience est présentée dans le livre Mécanique quantique de Jean Dalibard et al.
Mise en évidence de la quantification du carré du moment cinétique dans le cadre d’une expérience avec des molécules froides de éclairées par un laser de fréquence variable.
Cette expérience est présentée dans le livre Mécanique quantique de Jean Dalibard et al.
Harmoniques sphériques et représentations de
La théorie des représentations de groupe étudie la façon dont un groupe agit linéairement sur des espaces vectoriels complexes.
Par exemple, le groupe des rotations de l’espace, agit linéairement sur l’espace par composition à droite : définit l’action d’une rotation sur cet espace (par convention on compose par l’inverse de ).
On montre que cette représentation se décompose selon où désigne le sous-espace engendré par les (pour ). Les constituent les représentations irréductibles de .
En particulier, est stable par composition par les rotations : la -ème composante de s’obtient en composant à droite par la -ème composante de .
C’est pour cette raison que la représentation des light probes par leurs projections dans est insensible à un changement de repère orthonormé direct.
💡 Les représentations irréductibles de , l’algèbre de Lie de , sont elles indexées par des nombres entiers ou demi-entiers. Elles correspondent à des représentations du groupe et sont liées à la notion de spin.
Pour en savoir plus sur ces groupes et leurs représentations, vous pouvez lire Groupes et symétries d’Yvette Kosmann-Schwarzbach, dont un chapitre est dédié aux harmoniques sphériques.
Vous pouvez commenter cette entrée sur Bluesky, Twitter ou Mathstodon.
N'hésitez pas également à m'envoyer un email (thomas@lipsum.dev).
Maths et applications, avec les mains et avec du code 💻
Suivre sur Twitter
